Câu hỏi
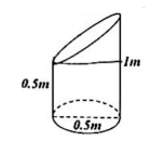
Một khối gỗ hình trụ đường kính 0,5m và chiều cao 1m. Người ta đã cắt khối gỗ, phần còn lại như hình vẽ bên có thể tích là V. Tính V?
- A
\(\frac{3\pi }{16}{{m}^{3}}\)
- B
\(\frac{5\pi }{64}{{m}^{3}}\)
- C
\(\frac{3\pi }{64}{{m}^{3}}\)
- D \(\frac{\pi }{16}{{m}^{3}}\)
Phương pháp giải:
Thể tích V bằng thể tích ban đầu của khối gỗ trừ đi thể tích phần khối gỗ bị cắt bỏ.
\({{V}_{tru}}=\pi {{r}^{2}}h\), trong đó \(r;h\) lần lượt là bán kính đáy và chiều cao của hình trụ.
Lời giải chi tiết:
Thể tích ban đầu của khối gỗ là \(V=\pi .0,{{25}^{2}}.1=\frac{\pi }{16}\).
Thể tích khối trụ bị cắt bỏ bằng \(\frac{1}{2}\) thể tích của khối trục có chiều cao 0,5m và bán kính đáy 0,25m.
\(\Rightarrow V'=\frac{1}{2}\pi .0,{{25}^{2}}.0,5=\frac{\pi }{64}\).
Vậy thể tích phần còn lại của khối gỗ là \(V-V'=\frac{\pi }{16}-\frac{\pi }{64}=\frac{3\pi }{64}\,\,{{m}^{3}}\)
Chọn C.