Câu hỏi
Cho hình chữ nhật ABCD có \(AB=a,BC=2a.\) Trên tia đối của tia AB lấy điểm O sao cho \(OA=x.\) Gọi d là đường thẳng đi qua O và song song với AD. Tìm x biết thể tích của hình tròn xoay tạo nên khi quay hình chữ nhật ABCD quanh d gấp ba lần thể tích hình cầu có bán kính bằng cạnh a.
- A
\(x=\frac{a}{2}.\)
- B
\(x=2a.\)
- C
\(x=a.\)
- D \(x=\frac{3a}{2}.\)
Phương pháp giải:
Sử dụng các công thức tính thể tích khối trụ và thể tích khối cầu.
Lời giải chi tiết:
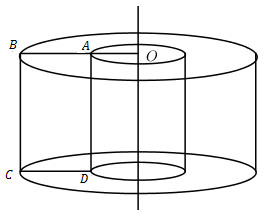
Khi xoay hình chữ nhật ABCD quanh đường thẳng d ta nhận được hai khối trụ.
Gọi \({{V}_{1}}\) là thể tích của khối trụ có đường cao BC và bán kính đáy OA.
Gọi \({{V}_{2}}\) là thể tích của khối trụ có đường cao BC và bán kính đáy OB.
Khi đó thể tích phần tròn xoay cần tính
\(\begin{align} V={{V}_{1}}-{{V}_{2}}=\pi O{{A}^{2}}AD-\pi O{{B}^{2}}AD \\ \,\,\,\,\,=\pi {{\left( a+x \right)}^{2}}.2a-\pi {{x}^{2}}.2a=\pi 2a\left( {{a}^{2}}+2ax \right) \\ \end{align}\)
Thể tích khối cầu có bán kính bằng a là \(V'=\frac{4}{3}\pi {{a}^{3}}\)
Ta có:
\(V=3V'\Leftrightarrow \pi .2a\left( {{a}^{2}}+2ax \right)=4\pi {{a}^{3}}\Leftrightarrow {{a}^{2}}+2ax=2{{a}^{2}}\Leftrightarrow x=\frac{a}{2}\)
Chọn A.







