Lời giải chi tiết:

Đáp án D

Theo đề ta vẽ được giản đồ vecto như hình vẽ

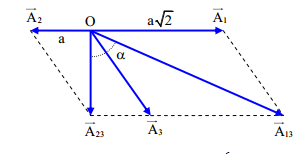
Ta có 

\({{\rm{W}}_1} = 2{W_2} = > {A_1} = {A_2}\sqrt 2 = > \left\{ \matrix{
{A_2} = a \hfill \cr
{A_1} = a\sqrt 2 \hfill \cr} \right.\)

Từ hình vẽ ta có : 

\(\left\{ \matrix{
A_{23}^2 = A_3^2 - {a^2} \hfill \cr
\cos \alpha = {{{A_{23}}} \over {{A_{13}}}} \hfill \cr} \right.\)

Theo đề :\({{{{\rm{W}}_{23}}} \over {{{\rm{W}}_{13}}}} = {1 \over 3} \Leftrightarrow {{A_{23}^2} \over {A_{13}^2}} = {1 \over 3} =  > \cos \alpha  = {1 \over {\sqrt 3 }} =  > \tan \alpha  = \sqrt 2 \)

Lại có :\(\tan \alpha  = {{a + a\sqrt 2 } \over {{A_{23}}}} =  > {A_{23}} = \left( {1,5 + \sqrt 2 } \right){a^2} =  > A_3^2 = \left( {2,5 + \sqrt 2 } \right){a^2}\)

Vì 

\(\left\{ \matrix{
x = {x_1} + {x_2} + {x_3} = {x_{23}} + {x_1} \hfill \cr
\buildrel {{x_{23}} \bot {x_1}} \over
\longrightarrow = > A_{th}^2 = A_{23}^2 + A_1^2\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{({A_1} = A\sqrt 2 )}^{(9)}} A_{th}^2 = \left( {3,5 + \sqrt 2 } \right){a^2} \hfill \cr} \right.\)

Ta có \({{{{\rm{W}}_{th}}} \over {{{\rm{W}}_{23}}}} = {{A_{th}^2} \over {{A_{23}}}} = {{\left( {3,5 + \sqrt 2 } \right){a^2}} \over {\left( {1,5 + \sqrt 2 } \right){a^2}}} \approx 1,7 =  > {{\rm{W}}_{th}} = 1,7W\)