Câu hỏi
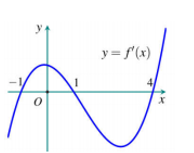
Cho hàm số \(y=f'\left( x \right)\) có đồ thị như hình vẽ bên dưới đây:
Tìm số điểm cực trị của hàm số \(y={{e}^{2f\left( x \right)+1}}+{{5}^{f\left( x \right)}}\).
- A 1
- B 2
- C 4
- D 3
Phương pháp giải:
Số điểm cực trị của hàm số \(y=f\left( x \right)\) là số nghiệm của phương trình \(f'\left( x \right)=0\) mà qua đó \(f'\left( x \right)\) đổi dấu.
Lời giải chi tiết:
Ta có \(y'=2f'\left( x \right).{{e}^{2f\left( x \right)+1}}+f'\left( x \right){{.5}^{f\left( x \right)}}=f'\left( x \right)\left[ 2{{e}^{2f\left( x \right)+1}}+{{5}^{f\left( x \right)}} \right]=0\)
Vì \(2{{e}^{2f\left( x \right)+1}}+{{5}^{f\left( x \right)}}>0\,\,\forall x\Rightarrow y'=0\Leftrightarrow f'\left( x \right)=0\Rightarrow \) Số điểm cực trị của hàm số \(y={{e}^{2f\left( x \right)+1}}+{{5}^{f\left( x \right)}}\) bằng số cực trị của hàm số \(y=f\left( x \right)\).
Dựa vào đồ thị hàm số \(y=f'\left( x \right)\) ta thấy hàm số \(y=f\left( x \right)\) có 3 điểm cực trị.
Vậy hàm số \(y={{e}^{2f\left( x \right)+1}}+{{5}^{f\left( x \right)}}\) cũng có 3 điểm cực trị.
Chọn D.