Câu hỏi
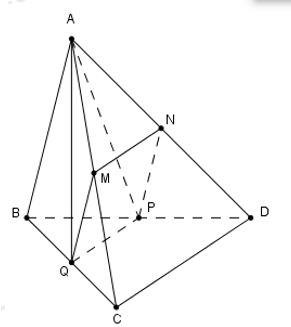
Cho khối tứ diện đều ABCD có thể tích V, M, N, P, Q lần lượt là trung điểm của AC, AD, BD, BC. Thể tích khối tứ diện AMNPQ là:
- A
\(\frac{V}{6}\)
- B
\(\frac{V}{3}\)
- C
\(\frac{V}{4}\)
- D \(\frac{\sqrt{2}V}{3}\)
Phương pháp giải:
Sử dụng tỉ lệ thể tích.
Lời giải chi tiết:
Tam giác BPQ và tam giác BCD đồng dạng theo tỉ số \(\frac{1}{2}\Rightarrow \frac{{{S}_{BPQ}}}{{{S}_{BCD}}}=\frac{1}{4}\Rightarrow \frac{{{V}_{A.BPQ}}}{{{V}_{A.BCD}}}=\frac{1}{4}\)
\(\Rightarrow {{V}_{A.PQCD}}=\frac{3}{4}{{V}_{ABCD}}\)
Ta có: \(\frac{{{V}_{A.MNP}}}{{{V}_{A.CDP}}}=\frac{AM}{AC}.\frac{AN}{AD}=\frac{1}{4}\Rightarrow {{V}_{A.MNP}}=\frac{1}{4}{{V}_{A.CDP}}\)
Ta có
\(\begin{align} {{S}_{PQCD}}=\frac{3}{4}{{S}_{BCD}};\,\,{{S}_{CDP}}=\frac{1}{2}{{S}_{BCD}} \\ \Rightarrow \frac{{{S}_{CDP}}}{{{S}_{PQCD}}}=\frac{2}{3}\Rightarrow {{V}_{A.CDP}}=\frac{2}{3}{{V}_{A.PQCD}}\Rightarrow {{V}_{A.MNP}}=\frac{1}{6}{{V}_{A.PQCD}} \\ \frac{{{V}_{A.MQP}}}{{{V}_{A.CQP}}}=\frac{AM}{AC}=\frac{1}{2}\Rightarrow {{V}_{A.MQP}}=\frac{1}{2}{{V}_{A.CQP}} \\ {{S}_{CPQ}}=\frac{1}{3}{{S}_{PQCD}}\Rightarrow {{V}_{A.CPQ}}=\frac{1}{3}{{V}_{A.PQCD}}\Rightarrow {{V}_{A.MQP}}=\frac{1}{6}{{V}_{A.PQCD}} \\ \end{align}\)
\(\Rightarrow {{V}_{A.MNPQ}}={{V}_{A.MNP}}+{{V}_{A.MQP}}=\frac{1}{6}{{V}_{A.PQCD}}+\frac{1}{6}{{V}_{A.PQCD}}=\frac{1}{3}{{V}_{A.PQCD}}=\frac{1}{4}{{V}_{ABCD}}=\frac{V}{4}\)
Chọn C.