Lời giải chi tiết:

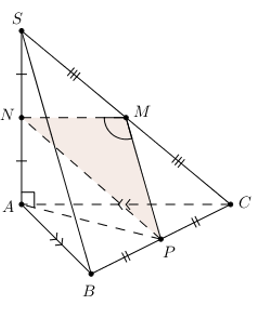
* Lấy M là trung điểm của SC.

Vẽ MN // AC, \(N\in SA,\,\,MP//SB,\,\,P\in BC\).

Ta có : \(\widehat{\left( SB;AC \right)}=\widehat{NMP}\).

* Tính

+ \(MN=\frac{AC}{2}=\frac{a}{2}\)

+ \(AP=\frac{a\sqrt{3}}{2},\,\,MP=\frac{SB}{2}=\frac{a\sqrt{2}}{2}\)

+ Tam giác vuông NAP : \(NP=\sqrt{\frac{3{{a}^{2}}}{4}+\frac{{{a}^{2}}}{4}}=a\)

+ \(\cos \widehat{M}=\frac{N{{P}^{2}}-M{{N}^{2}}-M{{P}^{2}}}{-2MN.MP}=\frac{{{a}^{2}}-\frac{{{a}^{2}}}{4}-\frac{2{{a}^{2}}}{4}}{-2.\frac{a}{2}.\frac{a\sqrt{2}}{2}}=-\frac{1}{2\sqrt{2}}\)

Chọn đáp án C.