Câu hỏi
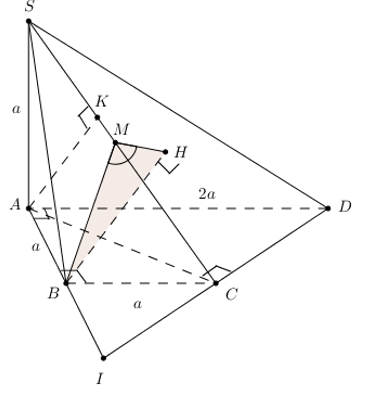
Chóp S.ABCD, \(SA\bot \left( ABCD \right),\,\,SA=a\). ABCD là hình thang vuông ở A, D. \(AD=DC=\frac{AB}{2}=a\). Tính \(\widehat{\left( \left( SCD \right);\left( SBC \right) \right)}\).
- A \({{30}^{0}}\)
- B \({{45}^{0}}\)
- C \({{60}^{0}}\)
- D \({{90}^{0}}\)
Lời giải chi tiết:
* Vẽ \(DH\bot \left( SBC \right)\).
Vẽ \(HM\bot SC\Rightarrow \widehat{\left( \left( SCD \right);\left( SBC \right) \right)}=\widehat{M}\).
* Nối \(AD\cap BC=I\). Ta có :
\(DH=d\left( D;\left( SBC \right) \right)=\frac{1}{2}d\left( A;\left( SBC \right) \right)=\frac{1}{2}AK\) \(\begin{align}+\,\,\frac{1}{A{{K}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{C}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{2{{a}^{2}}} \\ \Rightarrow AC=\frac{a\sqrt{6}}{3}\Rightarrow DH=\frac{a\sqrt{6}}{6} \\ \end{align}\).
+ Tam giác vuông SCD :
\(\begin{align}\frac{1}{D{{M}^{2}}}=\frac{1}{S{{D}^{2}}}+\frac{1}{C{{D}^{2}}}=\frac{1}{2{{a}^{2}}}+\frac{1}{{{a}^{2}}}=\frac{3}{2{{a}^{2}}}\Rightarrow DM=\frac{a\sqrt{6}}{3} \\ \Rightarrow \sin\widehat{M}=\frac{DH}{DM}=\frac{\frac{a\sqrt{6}}{6}}{\frac{a\sqrt{6}}{3}}=\frac{1}{2}\Rightarrow \widehat{M}={{30}^{0}} \\ \end{align}\)
Chọn đáp án A.