Câu hỏi
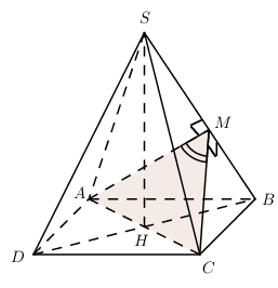
Chóp đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Tính \(\widehat{\left( \left( SAB \right);\left( SBC \right) \right)}\).
- A \(\arccos \frac{1}{2}\)
- B \(\arccos \frac{1}{6}\)
- C \(\arccos \frac{1}{3}\)
- D \(\arccos \frac{1}{4}\)
Lời giải chi tiết:
* Nhận xét: \(\Delta SAB=\Delta SBC\)
* Bước 1: Chọn \(A\in \left( P \right)\). Vẽ \(AM\bot \( giao tuyến SB.
\(\Rightarrow \widehat{\left( \left( SAB \right);\left( SBC \right) \right)}=\widehat{AMC}\)
* Bước 2: \(AM=MC=\frac{a\sqrt{3}}{2},AC=a\sqrt{2}\)
\(\begin{align} \Rightarrow \cos M=\frac{A{{C}^{2}}-M{{A}^{2}}-M{{C}^{2}}}{-2.MA.MC}=\frac{1}{3} \\ \Rightarrow \widehat{\left( \left( SAB \right);\left( SBC \right) \right)}=\arccos \frac{1}{3} \\ \end{align}\)
Đáp số: \(\arccos \frac{1}{3}\)
Câu hỏi trước
