Câu hỏi
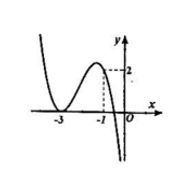
Cho đồ thị hàm bậc ba \(y=f\left( x \right)\) như hình vẽ. Hỏi đồ thị hàm số \(y=\frac{\left( {{x}^{2}}+4x+3 \right)\sqrt{{{x}^{2}}+x}}{x\left[ {{f}^{2}}\left( x \right)-2f\left( x \right) \right]}\) có bao nhiêu đường tiệm cận đứng?
- A 6
- B 3
- C 2
- D 4
Phương pháp giải:
Định nghĩa TCĐ của đồ thị hàm số \(y=f\left( x \right)\): Nếu \(\underset{x\to a}{\mathop{\lim }}\,y=\infty \Rightarrow x=a\) là TCĐ của đồ thị hàm số \(y=f\left( x \right)\).
Lời giải chi tiết:
Ta có \(y=\frac{\left( {{x}^{2}}+4x+3 \right)\sqrt{{{x}^{2}}+x}}{x\left[ {{f}^{2}}\left( x \right)-2f\left( x \right) \right]}=\frac{\left( x+1 \right)\left( x+3 \right)\sqrt{{{x}^{2}}+x}}{x.f\left( x \right)\left[ f\left( x \right)-2 \right]}\)
2ĐK:
\(\left\{ \begin{array}{l}x\left( {x + 1} \right) \ge 0\\x \ne 0\\f\left( x \right) \ne 0\\f\left( x \right) \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \in \left( { - \infty ; - 1} \right] \cup \left( {0; + \infty } \right)\\f\left( x \right) \ne 0\\f\left( x \right) \ne 2\end{array} \right.\)
.
Dựa vào đồ thị hàm số ta thấy phương trình \(f\left( x \right)=0\) có nghiệm kép \(x=-3\) và 1 nghiệm \(x=a\in \left( -1;0 \right)\), khi đó \(f\left( x \right)=m{{\left( x+3 \right)}^{2}}\left( x-a \right)\,\,\left( m\ne 0 \right)\).
Xét phương trình \(f\left( x \right)-2=0\Leftrightarrow f\left( x \right)=2,\) phương trình có 3 nghiệm phân biệt \(x=-1;\,\,x=b\in \left( -3;-1 \right);\,\,x=c\in \left( -\infty ;-3 \right)\), khi đó \(f\left( x \right)-2=n\left( x+1 \right)\left( x-b \right)\left( x-c \right)\).
Khi đó điều kiện xác định là : \(\left\{ \begin{align} x\in \left( -\infty ;-1 \right)\cup \left( 0;+\infty \right) \\ x\ne -3 \\ x\ne b;\,\,x\ne c \\ \end{align} \right.\)
\(\Rightarrow y=\frac{\left( x+1 \right)\left( x+3 \right)\sqrt{{{x}^{2}}+x}}{x.m{{\left( x+3 \right)}^{2}}\left( x-a \right).n\left( x+1 \right)\left( x-b \right)\left( x-c \right)}=\frac{\left( x+1 \right)\sqrt{{{x}^{2}}+x}}{mn.x\left( x+3 \right)\left( x-a \right)\left( x-b \right)\left( x-c \right)}\)
Khi \(x=a\in \left( 0;1 \right)\Rightarrow \) Hàm số không xác định.
Vây đồ thị hàm số có 4 TCĐ là \(x=0;\,\,x=-3;\,\,x=b;\,\,x=c\)
Chọn D.