Câu hỏi
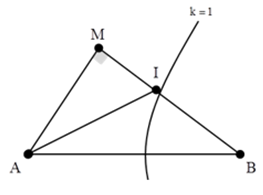
Trên mặt thoáng chất lỏng có hai nguồn kết hợp A, B cách nhau 20 cm, dao động với phương trình \({u_A} = {u_B} = 4\cos 20\pi t\) (với t tính bằng s). Tốc độ truyền sóng trên mặt chất lỏng là 40 cm/s. M là một điểm nằm trên mặt chất lỏng sao cho ∆AMB vuông tại M và MA = 12 cm, I là giao điểm của đường phân giác xuất phát từ góc A của ∆AMB với cạnh BM. Số điểm không dao động trên đoạn thẳng AI là
- A 7
- B 10
- C 6
- D 5
Lời giải chi tiết:
Đáp án C.
Bước sóng của song \(\lambda = {{2\pi {\rm{v}}} \over \omega } = {{2\pi .40} \over {20\pi }} = 4{\rm{cm}}{\rm{.}}\)
+ Số dãy cực đại giao thoa: \( - {{{\rm{AB}}} \over \lambda } \le {\rm{k}} \le {{{\rm{AB}}} \over \lambda } \leftrightarrow - 5 \le {\rm{k}} \le {\rm{5}} \to \) Có 11 dãy cực đại khi xảy ra giao thoa song nước.
+ AI là tia phân giác của góc
\(\widehat {{\rm{MAB}}} \to {{{\rm{MI}}} \over {{\rm{MA}}}} = {{{\rm{BI}}} \over {{\rm{BA}}}} \to {{{\rm{MI}}} \over {{\rm{BI}}}} = {{12} \over {20}} = {3 \over 5} \to \left\{ \matrix{
{\rm{MI = 6}} \hfill \cr
{\rm{BI}} = 10 \hfill \cr} \right.{\rm{cm}}{\rm{.}}\)
+ Ta có \(\cos \widehat {{\rm{ABM}}} = {{{\rm{MB}}} \over {{\rm{AB}}}} = {{16} \over {20}} = 0,8 \to \) áp dụng định lý cos trong ta có:
\({\rm{AI = }}\sqrt {{\rm{A}}{{\rm{B}}^2} + {\rm{I}}{{\rm{B}}^2} - 2{\rm{AB}}{\rm{.IBcos}}\widehat {{\rm{ABM}}}} = \sqrt {{{20}^2} + {{10}^2} - 2.20.10.0,8} = 6\sqrt 5 {\rm{ cm}}{\rm{.}}\)
Xét tỉ số \({{{\rm{AI - BI}}} \over \lambda } = {{6\sqrt 5 - 10} \over 4} \approx 0,85 \to \) Trên AI có 6 điểm không dao động ứng với \( - 5 \le {\rm{k}} \le {\rm{0}}{\rm{.}}\)