Môn Lý - Lớp 12
40 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng
Câu hỏi
Ba con lắc lò xo 1,2,3 đặt thẳng đứng cách đều nhau theo thứ tự 1,2,3. Ở vị trí cân bằng ba vật có cùng độ cao. Con lắc thứ nhất dao động có phương trình x1 = 3cos(20pt + $\frac{\pi }{2}$) (cm), con lắc thứ hai dao động có phương trình x2 = 1,5cos(20pt) (cm). Hỏi con lắc thứ ba dao động có phương trình nào thì ba vật luôn luôn nằm trên một đường thẳng?
- A x3 = 3$\sqrt 2 $cos(20pt - $\frac{\pi }{4}$) (cm).
- B x3 = $\sqrt 2 $cos(20pt - $\frac{\pi }{4}$) (cm).
- C x3 = 3$\sqrt 2 $cos(20pt - $\frac{\pi }{2}$) (cm).
- D x3 = 3$\sqrt 2 $cos(20pt -+$\frac{\pi }{4}$) (cm).
Lời giải chi tiết:
Đáp án A
Để ba vật luôn nằm trên một đường thẳng thì ${x_2} = \frac{{{x_1} + {x_3}}}{2}$ hay x3 = 2x2 – x1
→ Dao động của m3 là tổng hợp của 2 dao động điều hòa cùng phương, cùng tần số.
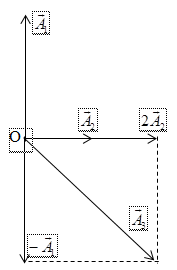
Dùng phương pháp giản đồ Fre-nen: ${\vec A_3} = 2{\vec A_2} + ( - {\vec A_1})$
Từ giản đồ suy ra: A3 = $\sqrt {{{(2{A_2})}^2} + A_1^2} $ = 3$\sqrt 2 $cm
Dễ thấy φ3 = - π/4 rad → x3 = 3$\sqrt 2 $cos(20pt - $\frac{\pi }{4}$) (cm).
(hoặc dùng máy tính tổng hợp dao động ).
Câu hỏi trước
