Phương pháp giải:

Gọi số phức, áp dụng bất đẳng thức Bunhiacopxki để tìm giá trị lớn nhất 

Lời giải chi tiết:

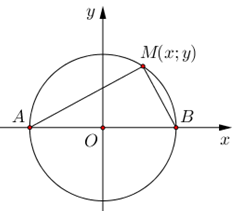
Cách 1. Gọi \(z=x+yi\,\,\left( x,y\in \mathbb{R} \right)\Rightarrow \)\(M\left( x;y \right)\).

Và \(A\left( -\,1;0 \right),\,B\left( 1;0 \right)\).

Ta có \(\left| z \right|=1\Rightarrow \left| x+yi \right|=1\Leftrightarrow {{x}^{2}}+{{y}^{2}}=1.\) \(\Rightarrow M\) thuộc đường tròn đường kính \(AB\). \(\Rightarrow M{{A}^{2}}+M{{B}^{2}}=A{{B}^{2}}=4.\)

Khi đó, theo Bunhiacopxki, ta có \(T=MA+2MB\le \sqrt{\left( {{1}^{2}}+{{2}^{2}} \right)\left( M{{A}^{2}}+M{{B}^{2}} \right)}=\sqrt{5.4}=2\sqrt{5}\)

Vậy giá trị lớn nhất của biểu thức \(\max T=2\sqrt{5}\).

Cách 2. Đặt \(z=x+yi\,\,\left( x,y\in \mathbb{R} \right)\Rightarrow \left| z+1 \right|=\sqrt{{{\left( x+1 \right)}^{2}}+{{y}^{2}}}\) và \(\left| z-1 \right|=\sqrt{{{\left( x-1 \right)}^{2}}+{{y}^{2}}}\).

Mặt khác \(\left| z \right|=1\Leftrightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}=1\Leftrightarrow {{x}^{2}}+{{y}^{2}}=1\), khi đó \(T=\sqrt{{{\left( x+1 \right)}^{2}}+{{y}^{2}}}+2\sqrt{{{\left( x-1 \right)}^{2}}+{{y}^{2}}}\) \(\Leftrightarrow T\le \sqrt{\left( {{1}^{2}}+{{2}^{2}} \right)\left[ {{\left( x+1 \right)}^{2}}+{{y}^{2}}+{{\left( x-1 \right)}^{2}}+{{y}^{2}} \right]}=\sqrt{10\left( {{x}^{2}}+{{y}^{2}}+1 \right)}=2\sqrt{5}\Rightarrow \max T=2\sqrt{5}.\)

Chọn A