Câu hỏi
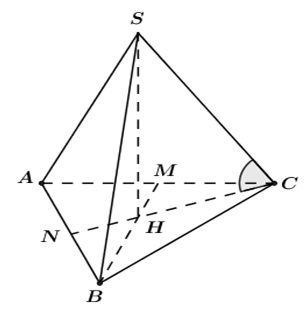
Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \(a,\) đường cao \(SH=\frac{a\sqrt{3}}{3}.\) Tính góc giữa cạnh bên và mặt đáy của hình chóp.
- A \({{45}^{0}}.\)
- B \({{30}^{0}}.\)
- C \({{75}^{0}}.\)
- D \({{60}^{0}}.\)
Phương pháp giải:
Dựng hình, xác định góc giữa cạnh bên và mặt đáy, đưa vào tam giác vuông tính góc
Lời giải chi tiết:
Vì \(S.ABC\) là hình chóp tam giác đều \(\Rightarrow \) \(H\) là tâm đường tròn ngoại tiếp \(\Delta \,ABC\)
Suy ra \(CH\) là hình chiếu của \(SC\) trên \(\left( ABC \right)\) \(\Rightarrow \,\,\widehat{\left( SC;\left( ABC \right) \right)}=\widehat{\left( SC;CH \right)}=\widehat{SCH}.\)
Tam giác \(SCH\) vuông tại \(H\) ta có : \(\tan \widehat{SCH}=\frac{SH}{CH}=\frac{a\sqrt{3}}{3}:\frac{a\sqrt{3}}{3}=1\Rightarrow \widehat{SCH}={{45}^{0}}.\)
Vậy góc giữa cạnh bên \(SC\) và mặt phẳng đáy bằng \({{45}^{0}}.\)
Chọn A