Câu hỏi
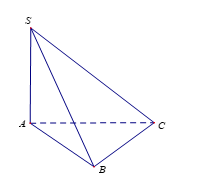
Cho hình chóp \(S.ABC\) có \(SA\bot \left( ABC \right)\); tam giác ABC đều cạnh \(a\) và \(SA=a\) (tham khảo hình vẽ bên). Tìm góc giữa đường thẳng SC và mặt phẳng \(\left( ABC \right).\)
- A
\(60{}^\circ \)
- B
\(45{}^\circ \)
- C
\(135{}^\circ \)
- D \(90{}^\circ \)
Phương pháp giải:
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Lời giải chi tiết:
\(\widehat{SC;\left( ABC \right)}=\widehat{\left( SC;AC \right)}=\widehat{SCA}\)
Tam giác SAC vuông cân tại A \(\Rightarrow \widehat{SCA}={{45}^{0}}\).
Chọn B.
Câu hỏi trước
