Phương pháp giải:

 Xét phương trình \(y'=0\Rightarrow \) các nghiệm của phương trình thuộc \(\left[ 1;3 \right]\). Lập BBT và suy ra GTLN của hàm số trên [1;3]

Lời giải chi tiết:

TXĐ: D = R. Ta có \(y'=3a{{x}^{2}}+c\)

Hàm số có \(\underset{\left( -\infty ;0 \right)}{\mathop{\min }}\,f\left( x \right)=f\left( -2 \right)\Rightarrow x=-2\) là 1 cực trị của hàm số \(\Rightarrow x=-2\) là một nghiệm của phương trình \(y'=0\).

TH1: c = 0 \(\Rightarrow a=0\,\,\left( ktm \right)\)

TH2: \(c\ne 0\Rightarrow \left[ \begin{align} & x=-\sqrt{-\frac{c}{3a}}=-2 \\ & x=\sqrt{-\frac{c}{3a}}=2\in \left[ 1;3 \right]\Rightarrow c=-12a \\ \end{align} \right.\)

\(\underset{\left( -\infty ;0 \right)}{\mathop{\min }}\,f\left( x \right)=f\left( -2 \right)\Rightarrow a<0\)

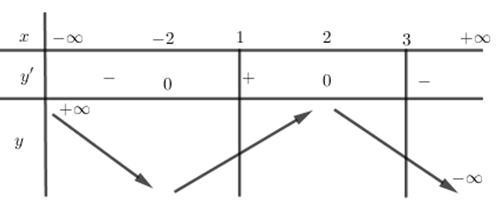
BBT ở hình vẽ bên:

\(\Rightarrow \underset{\left[ 1;3 \right]}{\mathop{\operatorname{m}ax}}\,f\left( x \right)=f\left( 2 \right)=8a+2c+d=8a-24a+d=-16a+d\)

Chọn B.