Câu hỏi
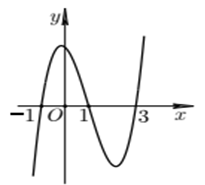
Cho hàm bậc bốn \(y=f\left( x \right)\). Hàm số \(y=f'\left( x \right)\) có đồ thị như hình bên. Số điểm cực đại của hàm số \(f\left( \sqrt{{{x}^{2}}+2x+2} \right)\) là
- A 1
- B 2
- C 4
- D 3
Phương pháp giải:
+) Đặt \(g\left( x \right)=f\left( \sqrt{{{x}^{2}}+2x+2} \right)\)
+) Tìm số nghiệm của phương trình \(g'\left( x \right)=0\) (không là nghiệm bội chẵn).
+) Lập BBT và kết luận điểm cực đại của hàm số.
Lời giải chi tiết:
Quan sát đồ thị hàm số \(y=f'\left( x \right)\) ta thấy \(f'\left( x \right)=0\Leftrightarrow \left[ \begin{align} & x=-1 \\ & x=1 \\ & x=3 \\ \end{align} \right.\)
Đặt \(g\left( x \right)=f\left( \sqrt{{{x}^{2}}+2x+2} \right)\Rightarrow g'\left( x \right)=\frac{x+1}{\sqrt{{{x}^{2}}+2x+2}}f'\left( \sqrt{{{x}^{2}}+2x+2} \right)\)
\(\begin{array}{l}
g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
x + 1 = 0\\
f'\left( {\sqrt {{x^2} + 2x + 2} } \right) = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = - 1\\
\sqrt {{x^2} + 2x + 2} = - 1\,\,\,\left( {vn} \right)\\
\sqrt {{x^2} + 2x + 2} = 1\,\,\,\left( 1 \right)\\
\sqrt {{x^2} + 2x + 2} = 3\,\,\,\left( 2 \right)
\end{array} \right.\\
\left( 1 \right) \Leftrightarrow {x^2} + 2x + 2 = 1 \Leftrightarrow {x^2} + 2x + 1 = 0 \Leftrightarrow {\left( {x + 1} \right)^2} = 0 \Leftrightarrow x = - 1\\
\left( 2 \right) \Leftrightarrow {x^2} + 2x + 2 = 9 \Leftrightarrow x = - 1 \pm 2\sqrt 2
\end{array}\)
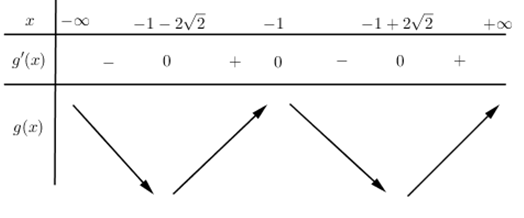
Nghiệm của phương trình (1) là nghiệm bội 2 nên không là cực trị của hàm số \(y=g\left( x \right)=f\left( \sqrt{{{x}^{2}}+2x+2} \right)\). Lập BBT của hàm số \(y=g\left( x \right)\):
Dựa vào BBT ta thấy hàm số \(y=g\left( x \right)\) đạt cực đại tại \(x=-1\).
Chọn A.