Phương pháp giải:

Lập BBT và suy ra GTNN của hàm số trên đoạn \(\left[ m+1;m+2 \right]\)

Lời giải chi tiết:

TXĐ: \(D=R\)

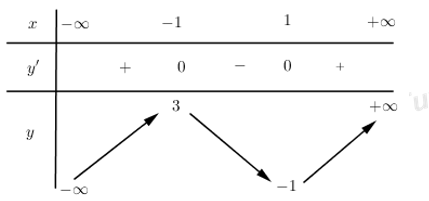
Ta có: \(y'=3{{x}^{2}}-3=0\Leftrightarrow x=\pm 1\)

BBT :

Với \(m>0\Rightarrow m+1>1\)

\(\Rightarrow \) Hàm số đồng biến trên \(\left[ m+1;m+2 \right]\Rightarrow \underset{\left[ m+1;m+2 \right]}{\mathop{\min }}\,f\left( x \right)=f\left( m+1 \right)={{\left( m+1 \right)}^{3}}-3\left( m+1 \right)+1<3\)

\(\Leftrightarrow \left( m+1-2 \right){{\left( m+1+1 \right)}^{2}}<0\Leftrightarrow m<1\)

Vậy \(m\in \left( 0;1 \right)\).

Chọn B.