Câu hỏi
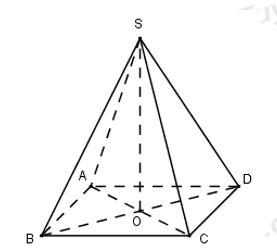
Cho khối chóp tứ giác đều có cạnh đáy bằng \(a\), cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho.
- A
\(V=\frac{\sqrt{14}{{a}^{3}}}{6}.\)
- B
\(V=\frac{\sqrt{14}{{a}^{3}}}{2}.\)
- C
\(V=\frac{\sqrt{2}{{a}^{3}}}{2}.\)
- D \(V=\frac{\sqrt{2}{{a}^{3}}}{6}.\)
Phương pháp giải:
\({{V}_{S.ABCD}}=\frac{1}{3}SO.{{S}_{ABCD}}\)
Lời giải chi tiết:
Gọi \(O=AC\cap BD\Rightarrow SO\bot \left( ABCD \right)\).
ABCD là hình vuông cạnh a \(\Rightarrow OB=\frac{BD}{2}=\frac{a\sqrt{2}}{2}\)
Xét tam giác vuông SOB có \(SO=\sqrt{4{{a}^{2}}-\frac{{{a}^{2}}}{2}}=\frac{a\sqrt{14}}{2}\)
\(\Rightarrow {{V}_{S.ABCD}}=\frac{1}{3}SO.{{S}_{ABCD}}=\frac{1}{3}\frac{a\sqrt{14}}{2}.{{a}^{2}}=\frac{{{a}^{3}}\sqrt{14}}{6}\)
Chọn A.
Câu hỏi trước
