Câu hỏi
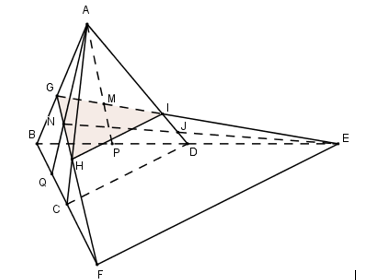
Cho tứ diện đều ABCD có cạnh bằng \(a\). Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích là V. Tính V.
- A
\(V=\frac{9\sqrt{2}{{a}^{3}}}{320}.\)
- B
\(V=\frac{3\sqrt{2}{{a}^{3}}}{320}.\)
- C
\(V=\frac{{{a}^{3}}\sqrt{2}}{96}.\)
- D \(V=\frac{3\sqrt{2}{{a}^{3}}}{80}.\)
Phương pháp giải:
Xác định thiết diện, sử dụng công thức tỉ số thể tích.
Lời giải chi tiết:
Trong (ABD) kéo dài EM cắt AB tại G, cắt AD tại I.
Trong (ABC) kéo dài GN cắt AC tại H.
Khi đó thiết diện của khối tứ diện khi cắt bởi mặt phẳng (EMN) là tam giác GHI.
(GHI) chia khối tứ diện thành hai phần là \(A.GHI\) và \(GHI.BCD\).
Gọi P, Q lần lượt là trung điểm của BD và BC.
Kéo dài GH cắt BC tại F.
Áp dụng định lí Menelaus:
Trong tam giác APD có: \(\frac{MA}{MP}.\frac{EP}{ED}.\frac{ID}{IA}=1\Leftrightarrow 2.\frac{3}{2}.\frac{ID}{IA}=1\Leftrightarrow \frac{ID}{IA}=\frac{1}{3}\Rightarrow \frac{AI}{AD}=\frac{3}{4}\)
Trong tam giác ABD có: \(\frac{GA}{GB}.\frac{EB}{ED}.\frac{ID}{IA}=1\Leftrightarrow \frac{GA}{GB}.2.\frac{1}{3}=1\Leftrightarrow \frac{GA}{GB}=\frac{3}{2}\Rightarrow \frac{AG}{AB}=\frac{3}{5}\)
Trong tam giác ABQ có: \(\frac{GA}{GB}.\frac{FB}{FQ}.\frac{NQ}{NA}=1\Leftrightarrow \frac{FB}{FQ}.\frac{3}{2}.\frac{1}{2}=1\Leftrightarrow \frac{FB}{FQ}=\frac{4}{3}\Rightarrow \frac{BQ}{BF}=\frac{1}{4}\Rightarrow \frac{BC}{BF}=\frac{1}{2}\Rightarrow C\) là trung điểm của BF \(\Rightarrow CD//EF\)
\(\left\{ \begin{align} \left( GHI \right)\cap \left( BCD \right)=EF \\ \left( GHI \right)\cap \left( ACD \right)=HI \\ \left( BCD \right)\cap \left( ACD \right)=CD \\ \end{align} \right.\Rightarrow EF//HI//CD\Rightarrow \frac{AH}{AC}=\frac{AI}{AD}=\frac{3}{4}\)
Vậy \(\frac{{{V}_{A.GHI}}}{{{V}_{A.BCD}}}=\frac{AG}{AB}.\frac{AH}{AC}.\frac{AI}{AD}=\frac{3}{5}.\frac{3}{4}.\frac{3}{4}=\frac{27}{80}\)
Thể tích tứ diện đều cạnh a \({{V}_{A.BCD}}=\frac{{{a}^{3}}\sqrt{2}}{12}\Rightarrow {{V}_{A.GHI}}=\frac{9\sqrt{2}{{a}^{3}}}{320}\) .
Chọn A.