Câu hỏi
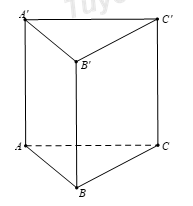
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có \(BB'=a\), đáy ABC là tam giác vuông cân tại B và \(AC=a\sqrt{2}\) (tham khảo hình vẽ bên). Tính thể tích V của khối lăng trụ đã cho.
- A
\(V={{a}^{3}}.\)
- B
\(V=\frac{{{a}^{3}}}{6}.\)
- C
\(V=\frac{{{a}^{3}}}{3}.\)
- D \(V=\frac{{{a}^{3}}}{2}.\)
Phương pháp giải:
\({{V}_{ABC.A'B'C'}}=BB'.{{S}_{ABC}}\)
Lời giải chi tiết:
Tam giác ABC vuông cân tại B \(\Rightarrow AB=BC=\frac{AC}{\sqrt{2}}=a\Rightarrow {{S}_{ABC}}=\frac{1}{2}{{a}^{2}}\)
\(\Rightarrow {{V}_{ABC.A'B'C'}}=BB'.{{S}_{ABC}}=\frac{{{a}^{3}}}{2}\)
Chọn D.
Câu hỏi trước
