Câu hỏi
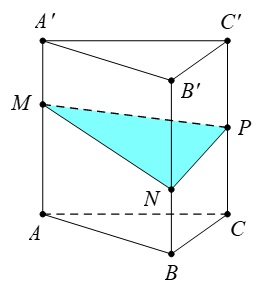
Cho hình lăng trụ tam giác \(ABC.{A}'{B}'{C}'\). Gọi \(M,\,\,N,\,\,P\) lần lượt là các điểm thuộc các cạnh \(A{A}',\,\,B{B}',\,\,C{C}'\) sao cho \(AM=2M{A}',\,\,N{B}'=2NB,\,\,PC=P{C}'.\) Gọi \({{V}_{1}},\,\,{{V}_{2}}\) lần lượt là thể tích của hai khối đa diện \(ABCMNP\) và \({A}'{B}'{C}'MNP.\) Tính tỉ số \(\dfrac{{{V}_{1}}}{{{V}_{2}}}.\)
- A \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=2.\)
- B \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{1}{2}.\)
- C \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=1.\)
- D \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{2}{3}.\)
Phương pháp giải:
Chia thành các khối đa diện nhỏ để tính thể tích
Lời giải chi tiết:
Đặt \(V={{V}_{ABC.{A}'{B}'{C}'}}.\)
Ta có \({{V}_{ABCMNP}}={{V}_{P.ABNM}}+{{V}_{P.ABC}},\) mặt khác: \(\bullet \,\,\,{{V}_{P.ABC}}=\dfrac{1}{3}.d\left( P;\left( ABC \right) \right).{{S}_{\Delta \,ABC}}=\dfrac{1}{6}.d\left( C;\left( ABC \right) \right).{{S}_{\Delta \,ABC}}=\dfrac{V}{6}.\)
\(\bullet \,\,\,\dfrac{{{S}_{ABNM}}}{{{S}_{AB{B}'{A}'}}}=\dfrac{AM+BN}{A{A}'+B{B}'}=\dfrac{\dfrac{2}{3}A{A}'+\dfrac{1}{3}B{B}'}{A{A}'+B{B}'}=\dfrac{1}{2}\Rightarrow \,\,{{V}_{P.ABNM}}=\dfrac{1}{2}{{V}_{C.AB{B}'{A}'}}.\)
Mà \({{V}_{C.AB{B}'{A}'}}=\dfrac{2}{3}V\) suy ra \({{V}_{P.ABNM}}=\dfrac{1}{2}.\dfrac{2}{3}V=\dfrac{V}{3}.\)
Khi đó \({{V}_{ABCMNP}}=\dfrac{V}{6}+\dfrac{V}{3}=\dfrac{V}{2}.\)
Vậy \(\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{V}{2}:\dfrac{V}{2}=1.\)
Chọn C .