Câu hỏi
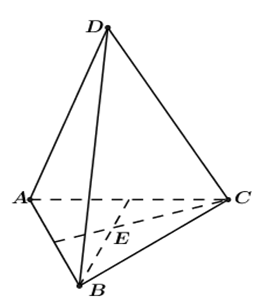
Cho mặt cầu \(\left( S \right)\) bán kính \(R=5\,\,cm.\) Mặt phẳng \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) có chu vi bằng \(8\pi \,\,cm.\) Bốn điểm \(A,\,\,B,\,\,C,\,\,D\) thay đổi sao cho \(A,\,\,B,\,\,C\) thuộc đường tròn \(\left( C \right),\) điểm \(D\) thuộc \(\left( S \right)\) (không thuộc đường tròn \(\left( C \right)\)) và tam giác \(ABC\) là tam giác đều. Tính thể tích lớn nhất của tứ diện \(ABCD.\)
- A \(32\sqrt{3}\,\,c{{m}^{3}}.\)
- B \(60\sqrt{3}\,\,c{{m}^{3}}.\)
- C \(20\sqrt{3}\,\,c{{m}^{3}}.\)
- D \(96\sqrt{3}\,\,c{{m}^{3}}.\)
Phương pháp giải:
Dựng hình, xác định vị trí điểm để thể tích lớn nhất
Lời giải chi tiết:
Gọi \(E\) là tâm đường tròn \(\left( C \right)\)\(\Rightarrow \)
Bán kính của \(\left( C \right)\) là \(r=\frac{C}{2\pi }=4\)
Mà \(\left( C \right)\) là đường tròn ngoại tiếp \(\Delta \,ABC\)\(\Rightarrow \,\,AB=\frac{3r}{\sqrt{3}}=4\sqrt{3}\Rightarrow \,\,{{S}_{\Delta \,ABC}}=\frac{A{{B}^{2}}\sqrt{3}}{4}=12\sqrt{3}.\)
Để \({{V}_{ABCD}}\) lớn nhất \(\Leftrightarrow \) \(E\) là hình chiếu của \(D\) trên \(mp\,\,\left( ABCD \right),\) tức là \(IE\cap \left( S \right)=D.\)
Với \(I\) là tâm mặt cầu \(\left( S \right)\)\(\Rightarrow \,\,DE=R+IE=R+\sqrt{{{R}^{2}}-{{r}^{2}}}=5+\sqrt{{{5}^{2}}-{{4}^{2}}}=8.\)
Vậy thể tích cần tính là \({{V}_{ABCD}}=\frac{1}{3}.DE.{{S}_{\Delta \,ABC}}=\frac{8}{3}.12\sqrt{3}=32\sqrt{3}\,\,c{{m}^{3}}.\)
Chọn A