Câu hỏi
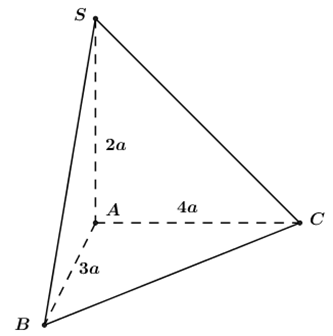
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( ABC \right).\) Biết \(SA=2a\) và tam giác \(ABC\) vuông tại \(A\) có \(AB=3a,\,\,AC=4a.\) Tính thể tích khối chóp \(S.ABC\) theo \(a.\)
- A \(12{{a}^{3}}.\)
- B \(6{{a}^{3}}.\)
- C \(8{{a}^{3}}.\)
- D \(4{{a}^{3}}.\)
Phương pháp giải:
Công thức tính thể tích khối chóp \(V=\frac{1}{3}Sh\)
Lời giải chi tiết:
Thể tích khối chóp \(S.ABC\) là \(V=\frac{1}{3}.SA.{{S}_{\Delta \,ABC}}=\frac{1}{3}.SA.\frac{1}{2}.AB.AC=\frac{2a.3a.4a}{6}=4{{a}^{3}}.\)
Chọn D
Câu hỏi trước
