Phương pháp giải:

- Sử dụng sự tương giao giữa hai đồ thị hàm số để đánh giá số nghiệm của phương trình.

Lời giải chi tiết:

\({{x}^{3}}-12x+m-2=0\Leftrightarrow {{x}^{3}}-12x-2=-m\)  (*)

Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị hàm số \(y={{x}^{3}}-12x-2\) và đường thẳng \(y=-m\).

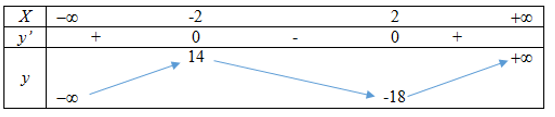
Xét \(y={{x}^{3}}-12x-2\) có \(y'=3{{x}^{2}}-12=0\Leftrightarrow x=\pm 2\)

Bảng biến thiên:

Khi đó, \(y={{x}^{3}}-12x-2\) cắt \(y=-m\) tại 3 điểm phân biệt \(\Leftrightarrow -18<-m<14\Leftrightarrow -14<m<18\).

Chọn: C