Câu hỏi
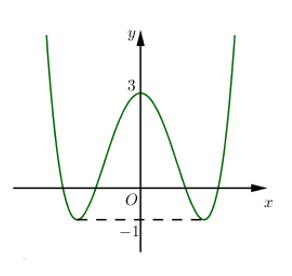
Cho hàm số \(y=\frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3\) có đồ thị như hình dưới. Tổng tất cả các giá trị nguyên của tham số m để phương trình \(\left| {{x}^{4}}-8{{x}^{2}}+12 \right|=m\) có 8 nghiệm phân biệt là:
- A 3
- B 10
- C 0
- D 6
Phương pháp giải:
\(\left| {{x}^{4}}-8{{x}^{2}}+12 \right|=m\Leftrightarrow \left| \frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3 \right|=\frac{m}{4}\)
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y=\left| \frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3 \right|\) và đường thẳng \(y=\frac{m}{4}\)
Lời giải chi tiết:
\(\left| {{x}^{4}}-8{{x}^{2}}+12 \right|=m\Leftrightarrow \left| \frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3 \right|=\frac{m}{4}\)
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y=\left| \frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3 \right|\) và đường thẳng \(y=\frac{m}{4}\)
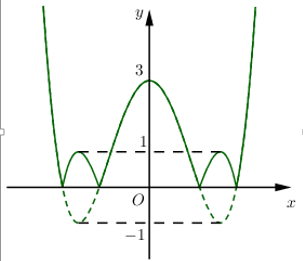
Từ đồ thị hàm số \(y=\frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3\) ta suy ra đồ thị hàm số \(y=\left| \frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3 \right|\) có hình dạng như sau:
Dựa vào đồ thị hàm số ta thấy để đường thẳng \(y=\frac{m}{4}\) cắt đồ thị hàm số \(y=\left| \frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3 \right|\) tại 8 điểm phân biệt \(\Leftrightarrow 0<\frac{m}{4}<1\Leftrightarrow 0<m<4\overset{m\in Z}{\mathop{\Rightarrow }}\,m\in \left\{ 1;2;3 \right\}\Rightarrow \sum{m}=6\)
Chọn D.