Câu hỏi
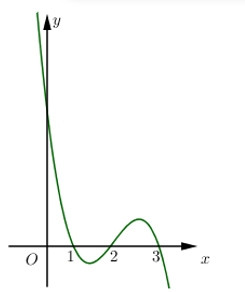
Cho hàm số \(f\left( x \right)\) xác định trên R và hàm số \(y=f'\left( x \right)\) có đồ thị như hình bên dưới:
Xét các khẳng định sau:
(I) Hàm số \(y=f\left( x \right)\) có ba cực trị.
(II) Phương trình \(f\left( x \right)=m+2018\) có nhiều nhất ba nghiệm.
(III) Hàm số \(y=f\left( x+1 \right)\) nghịch biến trên khoảng \(\left( 0;1 \right)\).
Số khẳng định đúng là:
- A 1
- B 2
- C 0
- D 3
Phương pháp giải:
Từ đồ thị hàm số \(y=f'\left( x \right)\) lập BBT của đồ thị hàm số \(y=f\left( x \right)\) và kết luận.
Lời giải chi tiết:
Ta có \(f'\left( x \right)=0\Leftrightarrow \left[ \begin{align}x=1 \\x=2 \\x=3 \\\end{align} \right.\)
BBT:
Từ BBT ta thấy (I) đúng, (II) sai.
Với \(x\in \left( 0;1 \right)\Rightarrow x+1\in \left( 1;2 \right)\Rightarrow f'\left( x+1 \right)<0\Rightarrow \) Hàm số \(y=f\left( x+1 \right)\) nghịch biến trên khoảng \(\left( 0;1 \right)\).
\(\Rightarrow \left( III \right)\) đúng.
Vậy có hai khẳng định đúng.
Chọn B.