Câu hỏi
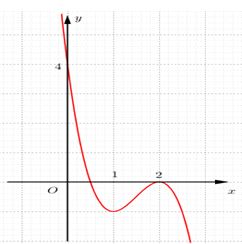
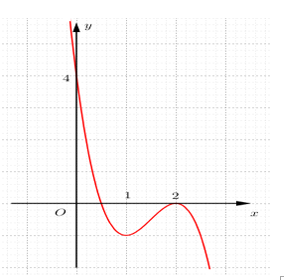
Cho hàm số \(y=-2{{x}^{3}}+b{{x}^{2}}+cx+d\) có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?
- A
\({{c}^{2}}<{{b}^{2}}+{{d}^{2}}\)
- B
\(b+d<c\)
- C
\(b+c+d=1\)
- D \(bcd=-144\)
Phương pháp giải:
Dựa vào các điểm mà đồ thị hàm số đi qua.
Lời giải chi tiết:
Đồ thị hàm số đi qua điểm \(\left( 0;4 \right)\Rightarrow d=4\)
Đồ thị hàm số đi qua điểm \(\left( 1;-1 \right)\Rightarrow -2+b+c+4=-1\Rightarrow b+c=-3\)
Đồ thị hàm số đi qua điểm \(\left( 2;0 \right)\Rightarrow -2.8+4b+2c+4=0\Leftrightarrow 2b+c=6\)
Từ đó ta suy ra \(\left\{ \begin{align}b=9 \\c=-12 \\\end{align} \right.\Rightarrow b+c+d=1\)
Chọn C.
Câu hỏi trước
