Câu hỏi
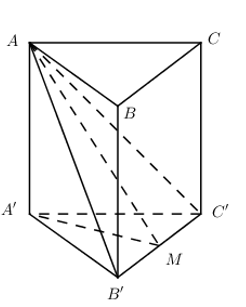
Cho khối lăng trụ đứng \(ABC.A'B'C’\) có đáy là tam giác cân \(ABC\) với \(AB=AC=2x,\,\,\widehat{BAC}={{120}^{0}}\), mặt phẳng \(\left( AB'C' \right)\) tạo với đáy một góc \({{30}^{0}}\). Tính thể tích \(V\) của khối lăng trụ đã cho?
- A
\(V=\frac{4{{x}^{3}}}{3}\)
- B
\(V=\frac{9{{x}^{3}}}{8}\)
- C
\(V=\frac{3{{x}^{3}}}{16}\)
- D \(V={{x}^{3}}\)
Phương pháp giải:
\({{V}_{ABC.A'B'C'}}=AA'{{.}_{A'B'C'}}\)
Lời giải chi tiết:
\(\Delta AA'B'=\Delta AA'C'\,\,\left( c.g.c \right)\Rightarrow AB'=AC’\) cân tại A.
Gọi M là trung điểm của B’C’ \(\Rightarrow AM\bot B'C’\).
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\left( {AB'C'} \right) \cap \left( {A'B'C'} \right) = B'C'\\\left( {AB'C'} \right) \supset AM \bot B'C'\\\left( {A'B'C'} \right) \supset A'M \bot B'C'\end{array} \right.\\ \Rightarrow \widehat {\left( {\left( {AB'C'} \right);\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AM;A'M} \right)} = \widehat {AMA'} = {30^0}\end{array}\)
Xét tam giác vuông A’B’M có \(A'M=A'B'.\cos 60=x\)
Xét tam giác vuông AMA’ có: \(AA'=A'M.\tan 30=\frac{x\sqrt{3}}{3}\)
\(\begin{align}{{S}_{A'B'C'}}=\frac{1}{2}A'B'.A'C'.\sin {{120}^{0}}=\frac{1}{2}.4{{x}^{2}}.\frac{\sqrt{3}}{2}={{x}^{2}}\sqrt{3} \\\Rightarrow {{V}_{ABC.A'B'C'}}=AA'{{.}_{A'B'C'}}=\frac{x\sqrt{3}}{3}.{{x}^{2}}\sqrt{3}={{x}^{3}} \\\end{align}\)
Chọn D.