Câu hỏi
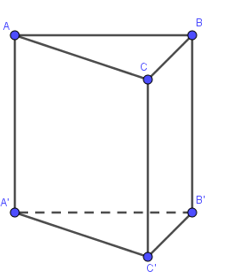
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy là một tam giác vuông tại \(A,\,\,\widehat{ACB}={{60}^{0}}\), \(AC=a,\,\,AA'=2a\). Thể tích khối lăng trụ theo a là
- A \({{a}^{3}}\sqrt{3}\).
- B \(\frac{{{a}^{3}}\sqrt{6}}{2}\).
- C \(\frac{{{a}^{3}}\sqrt{3}}{3}\).
- D \(\frac{{{a}^{3}}\sqrt{2}}{3}\).
Phương pháp giải:
Thể tích khối lăng trụ: \(V=Bh\), trong đó:
\(B:\) diện tích đáy, \(h:\) chiều cao.
Lời giải chi tiết:
Tam giác ABC vuông tại \(A,\,\,\widehat{ACB}={{60}^{0}}\)
\(\Rightarrow AB=AC.\tan \widehat{ACB}=a.\tan {{60}^{0}}=a\sqrt{3}\).
\({{S}_{ABC}}=\frac{1}{2}AB.AC=\frac{1}{2}.a\sqrt{3}.a=\frac{{{a}^{2}}\sqrt{3}}{2}\)
Thể tích khối lăng trụ: \(V={{S}_{ABC}}.AA'=\frac{{{a}^{2}}\sqrt{3}}{2}.2a={{a}^{3}}\sqrt{3}\)
Chọn: A
Câu hỏi trước
