Phương pháp giải:

sử dụng giản đồ vec to và định luật Ôm

Lời giải chi tiết:

Dựa vào biểu thức điện áp tức thời của cuộn dây và tụ, ta thấy u_dsớm pha \(\frac{\pi }{6} + \frac{{2\pi }}{3} = \frac{{5\pi }}{6}\) so với u_C . ta vẽ được giản đồ vecto như sau

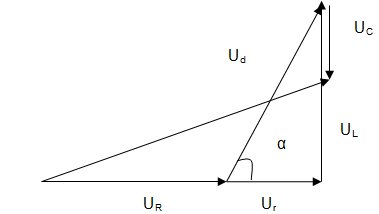
Từ giản đồ vecto thấy góc lệch giữa u_d và u_Clà: \(\alpha + \frac{\pi }{2} = \frac{{5\pi }}{6} = > \alpha = \frac{\pi }{3}\)

 Từ phương trình điện áp ta có   \({U_d} = 80\sqrt 3 V;{U_C} = 40V\)

Từ giản đồ vecto, ta có:

\(\eqalign{
& {U_r} = {U_d}.\cos \alpha = 80\sqrt 3 .\cos {\pi \over 3} = 40\sqrt 3 V \cr
& {U_L} = {U_d}.\sin \alpha = 80\sqrt 3 .\sin {\pi \over 3} = 120V \cr} \)

Ta có:

\(\begin{gathered}
U_{AB}^2 = {({U_R} + {U_r})^2} + {({U_L} - {U_C})^2} = {\left( {60\sqrt 3 + 40\sqrt 3 } \right)^2} + {\left( {120 - 40} \right)^2} \hfill \\
{U_{AB}} \approx 190,78V \hfill \\
\end{gathered} \)

Hệ số công suất được xác định bởi:

\(k = \cos \varphi = \frac{{R + r}}{Z} = \frac{{{U_R} + {U_r}}}{{{U_{AB}}}} = \frac{{60\sqrt 3 + 40\sqrt 3 }}{{190,78}} \approx 0,908\)