Câu hỏi
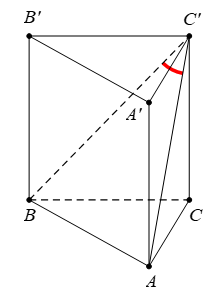
Cho khối lăng trụ đứng \(ABC.\,{A}'{B}'{C}'\) có đáy là tam giác \(ABC\) vuông tại \(A,\,\,AC=a,\,\,\widehat{ACB}={{60}^{0}}.\) Đường thẳng \(B{C}'\) tạo với mặt phẳng \(\left( A{A}'{C}'C \right)\) góc \({{30}^{0}}.\) Tính thể tích khối lăng trụ đã cho.
- A \(2{{a}^{3}}\sqrt{3}.\)
- B \({{a}^{3}}\sqrt{6}.\)
- C \(\frac{{{a}^{3}}\sqrt{3}}{2}.\)
- D \(\frac{{{a}^{3}}\sqrt{3}}{3}.\)
Phương pháp giải:
\(V=A{A}'\times {{S}_{\Delta ABC}}\)
Lời giải chi tiết:
Tam giác \(ABC\) vuông tại \(A,\) có \(AB=AC.\tan {{60}^{0}}=a\sqrt{3}\Rightarrow BC=2a.\)
Và \(AB\bot AC\) mà \(A{A}'\bot \left( ABC \right)\)\(\Rightarrow AB\bot mp\,\,\left( AC{C}'{A}' \right).\)
Khi đó \(\widehat{B{C}';\left( AC{C}'{A}' \right)}=\widehat{\left( B{C}';A{C}' \right)}=\widehat{BA{C}'}={{30}^{0}}\)\(\Rightarrow \)\(B{C}'=\frac{AB}{\sin {{30}^{0}}}=2a\sqrt{3}.\)
Tam giác \(BC{C}'\) vuông tại \(C,\) có \(C{C}'=\sqrt{B{{{{C}'}}^{2}}-B{{C}^{2}}}=2a\sqrt{2}.\)
Vậy thể tích khối lăng trụ \(ABC.\,{A}'{B}'{C}'\) là
\(V=A{A}'\times {{S}_{\Delta ABC}}=2a\sqrt{2}.\frac{{{a}^{2}}\sqrt{3}}{2}={{a}^{3}}\sqrt{6}.\)
Chọn B.