Phương pháp giải:

+) Kẻ \(AD\bot B'C\), xác định góc giữa mặt phẳng \(\left( AB'C \right)\) và mặt phẳng \(\left( BCC'B' \right)\).

+) Tính BB’.

+) Tính thể tích khối lăng trụ và suy ra thế tích \(AB'CA'C'\)

Lời giải chi tiết:

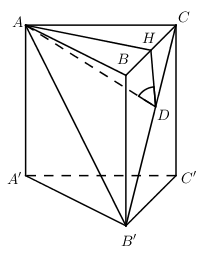
Gọi \(H\) là trung điểm của BC ta có

\(AH\bot BC\Rightarrow AH\bot \left( BCC'B' \right)\Rightarrow AH\bot B'C\)

Trong \(\left( AB'C \right)\) kẻ \(AD\bot B'C\)

\(\Rightarrow B'C\bot \left( AHD \right)\Rightarrow B'C\bot HD\)

Ta có :

\(\left\{ \begin{align}  \left( AB'C \right)\cap \left( BCC'B' \right)=B'C \\  \left( AB'C \right)\supset AD\bot B'C \\  \left( BCC'B' \right)\supset HD\bot B'C \\ \end{align} \right.\Rightarrow \widehat{\left( \left( AB'C \right);\left( BCC'B' \right) \right)}=\widehat{\left( AD;HD \right)}=\widehat{ADH}\) Ta có \(AH=\frac{AB}{2}=\frac{a\sqrt{6}}{2}\Rightarrow HD=AH.\cot 60=\frac{a\sqrt{2}}{2}\)

Dễ thấy \(\Delta CBB'\) đồng dạng với \(\Delta CDH\) (g.g)

\(\Rightarrow \frac{BB'}{HD}=\frac{CB'}{CH}\Rightarrow \frac{BB'}{\frac{a\sqrt{2}}{2}}=\frac{\sqrt{6{{a}^{2}}+BB{{'}^{2}}}}{\frac{a\sqrt{6}}{2}}\Leftrightarrow \sqrt{3}BB'=\sqrt{6{{a}^{2}}+BB{{'}^{2}}}\Leftrightarrow 2BB{{'}^{2}}=6{{a}^{2}}\Leftrightarrow BB'=a\sqrt{3}\)

Ta có : \(AB=AC=\frac{BC}{\sqrt{2}}=a\sqrt{3}\Rightarrow {{S}_{ABC}}=\frac{1}{2}AB.AC=\frac{3{{a}^{2}}}{2}\)

\(\begin{align}  \Rightarrow {{V}_{ABC.A'B'C'}}=BB'.{{S}_{ABC}}=a\sqrt{3}.\frac{3{{a}^{2}}}{2}=\frac{3\sqrt{3}{{a}^{3}}}{2} \\  {{V}_{AB'CA'C'}}+{{V}_{B'.ABC}}={{V}_{ABC.A'B'C'}}\Rightarrow {{V}_{AB'CA'C'}}={{V}_{ABC.A'B'C'}}-{{V}_{B'.ABC}}={{V}_{ABC.A'B'C'}}-\frac{1}{3}{{V}_{ABC.A'B'C'}}=\frac{2}{3}{{V}_{ABC.A'B'C'}} \\  \Rightarrow {{V}_{AB'CA'C'}}=\frac{2}{3}.\frac{3\sqrt{3}{{a}^{3}}}{2}={{a}^{3}}\sqrt{3} \\ \end{align}\) 

Chọn D.