Câu hỏi
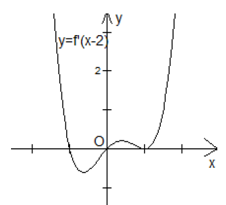
Cho hàm số \(y=f\left( x \right)\) có đạo hàm liên tục trên R, hàm số \(y=f'\left( x-2 \right)\) có đồ thị hàm số như hình bên. Số điểm cực trị của hàm số \(y=f\left( x \right)\) là :
- A 0
- B 2
- C 1
- D 3
Phương pháp giải:
Nhận xét : \(f'\left( x-2 \right)=f'\left( x \right)\)
Lời giải chi tiết:
Đồ thị hàm số \(y=f'(x)\) nhận được khi tịnh tiến đồ thị hàm số \(y=f'(x-2)\) sang trái theo trục \(Ox\) 2 đơn vị nên số cực trị của hàm số \(y=f(x)\) bằng số cực trị của hàm số \(y=f(x-2)\).
Ta thấy phương trình \(f'(x-2)=0\) có 3 nghiệm phân biệt tuy nhiên chỉ đổi dấu qua 2 nghiệm \(x=-1;x=0\), do đó đồ thị hàm số có 2 điểm cực trị.
Chọn B.
Câu hỏi trước
