Phương pháp giải:

Khoảng cách giữa hai điểm sáng được biểu diễn bởi phương trình: d = x₁ – x₂ = Acos(ωt + φ)

Với \(\tan \varphi  = {{{A_1}\sin {\varphi _1} - {A_2}\sin {\varphi _2}} \over {{A_1}\cos {\varphi _1} - {A_2}c{\rm{os}}{\varphi _2}}}\)

Sử dụng đường tròn lượng giác

Lời giải chi tiết:

+ Phương trình vận tốc của hai chất điểm: 

\(\left\{ \matrix{
{v_1} = 20\pi c{\rm{os}}\left( {5\pi t + {\pi \over 2}} \right) \hfill \cr
{v_2} = 20\pi \sqrt 3 c{\rm{os}}\left( {5\pi t + {\pi \over 6} + {\pi \over 2}} \right) = 20\pi \sqrt 3 c{\rm{os}}\left( {5\pi t + {{2\pi } \over 3}} \right) \hfill \cr} \right.\)

+ Ta có: d = x₁ – x₂ = Acos(ωt + φ)

Với: \(\tan \varphi  = {{4\sin 0 - 4\sqrt 3 \sin {\pi  \over 6}} \over {4\cos 0 - 4\sqrt 3 c{\rm{os}}{\pi  \over 6}}} = \sqrt 3  \Rightarrow \varphi  = {\pi  \over 3} \Rightarrow d = A\cos \left( {5\pi t + {\pi  \over 3}} \right) \Rightarrow {d_{\max }} = A \Leftrightarrow d =  \pm A\)

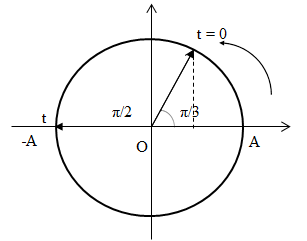
+ Thời điểm đầu tiên t hai điểm sáng cách xa nhau nhất được biểu diễn trên đường tròn lượng giác:

Góc quét được: \(\alpha  = {\pi  \over 6} + {\pi  \over 2} = {{2\pi } \over 3} \Rightarrow t = {\alpha  \over \omega } = {{{{2\pi } \over 3}} \over {5\pi }} = {2 \over {15}}s\)

+ Tại t = 2/15s tỉ số vận tốc của chất điểm 1 so với chất điểm 2: \({{{v_1}} \over {{v_2}}} = {{20\pi c{\rm{os}}\left( {5\pi .{2 \over {15}} + {\pi  \over 2}} \right)} \over {20\pi \sqrt 3 c{\rm{os}}\left( {5\pi .{2 \over {15}} + {{2\pi } \over 3}} \right)}} = {{ - {{\sqrt 3 } \over 2}} \over { - {{\sqrt 3 } \over 2}}} = 1\)