Phương pháp giải:

Sử dụng đường tròn lượng giác

Định luật bảo toàn cơ năng: W = Wđ + Wt

Lời giải chi tiết:

+ Phương trình dao động của hai con lắc lò xo: 

\(\left\{ \matrix{
{x_M} = Ac{\rm{os}}\left( {\omega t + {\varphi _M}} \right) \hfill \cr
{x_N} = A\sqrt 3 c{\rm{os}}\left( {\omega t + {\varphi _N}} \right) \hfill \cr} \right.\)

+ Khoảng cách giữa hai vật nặng của hai con lắc lò xo tại thời điểm t là: d = x_M – x_N = A_MN.cos(ωt + φ)

Với \({A_{MN}} = \sqrt {A_M^2 + A_N^2 - 2{A_M}{A_N}c{\rm{os}}\left( {{\varphi _M} - {\varphi _N}} \right)}  \Leftrightarrow \sqrt {{A^2} + {{\left( {A\sqrt 3 } \right)}^2} - 2A.A\sqrt 3 c{\rm{os}}\Delta \varphi } \)

+ Trong quá trình dao động, độ chênh lệch độ cao lớn nhất của hai vật là A:

\( \Rightarrow {\left[ {{A_{MN}}\cos \left( {\omega t + \varphi } \right)} \right]_{\max }} = A \Leftrightarrow \sqrt {{A^2} + {{\left( {A\sqrt 3 } \right)}^2} - 2A.A\sqrt 3 c{\rm{os}}\Delta \varphi }  = A \Rightarrow c{\rm{os}}\Delta \varphi  = {{\sqrt 3 } \over 2} \Rightarrow \Delta \varphi  = {\pi  \over 6}\) 

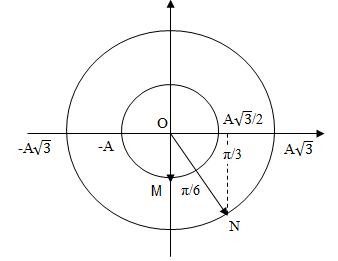
+ Động năng của con lắc M cực đại \({{\rm{W}}_{dM}} = {{k{A^2}} \over 2} = 0,12J\) khi vật M ở VTCB. Khi đó ta biểu diễn được vị trí của vật N được biểu diễn trên đường tròn lượng giác (M và N lệch pha nhau góc π/6).

+ Từ đường tròn lượng giác xác định được \({x_N} = A\sqrt 3 c{\rm{os}}{\pi  \over 3} = {{A\sqrt 3 } \over 2}\)

=> Động năng của con lắc N là:

\({{\rm{W}}_{dN}} = {{\rm{W}}_N} - {{\rm{W}}_{tN}} = {{kA_N^2} \over 2} - {{kx_N^2} \over 2} = {{k{{\left( {A\sqrt 3 } \right)}^2}} \over 2} - {{k{{\left( {{{A\sqrt 3 } \over 2}} \right)}^2}} \over 2} = \left( {3 - {3 \over 4}} \right){{k{A^2}} \over 2} = {9 \over 4}.0,12 = 0,27J\)