Câu hỏi
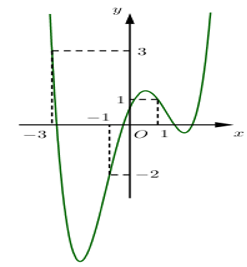
Cho hàm số \(y=f\left( x \right)\) xác định trên R. Đồ thị hàm số \(y=f'\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right)=f\left) x \right)-\frac{1}{3}{{x}^{3}}-\frac{3}{4}{{x}^{2}}+\frac{3}{2}x+2018\). Điểm cực tiểu của hàm số \(g\left( x \right)\) đoạn \(\left[ -3;1 \right]\) là:
- A \({{x}_{CT}}=-1\)
- B \({{x}_{CT}}=\frac{1}{2}\)
- C \({{x}_{CT}}=-2\)
- D \({{x}_{CT}}=0\)
Phương pháp giải:
Tính \(g'\left( x \right)\), tìm các nghiệm của phương trình \(g'\left( x \right)=0\).
Điểm \({{x}_{0}}\) được gọi là điểm cực tiểu của hàm số\(y=g\left( x \right)\) khi và chỉ khi \(g'\left( {{x}_{0}} \right)=0\) và qua điểm \(x={{x}_{0}}\) thì \(g'\left( x \right)\) đổi dấu từ âm sang dương.
Lời giải chi tiết:
\(g'\left( x \right)=f'\left( x \right)-{{x}^{2}}-\frac{3}{2}x+\frac{3}{2}=0\Leftrightarrow f'\left( x \right)={{x}^{2}}+\frac{3}{2}x-\frac{3}{2}\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=-1 \\ & x=-3 \\ \end{align} \right.\)
Khi \(x<1\) ta có: \(f'\left( x \right)>{{x}^{2}}+\frac{3}{2}x-\frac{3}{2}\Rightarrow g'\left( x \right)>0\) , khi \(x>1\) ta có \(f'\left( x \right)<{{x}^{2}}+\frac{3}{2}x-\frac{3}{2}\Rightarrow g'\left( x \right)<0\)
Qua \(x=1\(, \(g'\left( x \right)\) đổi dấu từ dương sang âm \(\Rightarrow x=1\) là điểm cực đại của đồ thị hàm số \(y=g\left( x \right)\)
Chứng minh tương tự ta được \(x=-1\) là điểm cực tiểu và \(x=-3\) là điểm cực đại của đồ thị hàm số \(y=g\left( x \right)\)
Chọn A.