Câu hỏi
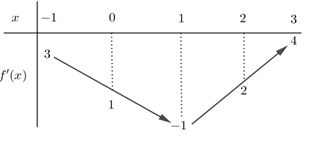
Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số \(y={f}'(x)\) được cho như hình vẽ bên. Hàm số \(y=f\left( 1-\frac{x}{2} \right)+x\) nghịch biến trên khoảng
- A \((2;4).\)
- B \((-4;-2).\)
- C \((-2;0).\)
- D \((0;2).\)
Phương pháp giải:
Tính \(g'\left( x \right)\), giải bất phương trình \(g'\left( x \right)<0\)
Lời giải chi tiết:
Ta có \(g\left( x \right)=f\left( 1-\frac{x}{2} \right)+x\Rightarrow {g}'\left( x \right)=-\,\frac{1}{2}.{f}'\left( 1-\frac{x}{2} \right)+1;\,\,\forall x\in R.\)
Xét bất phương trình \({g}'\left( x \right)<0\Leftrightarrow -\,\frac{1}{2}.{f}'\left( 1-\frac{x}{2} \right)+1<0\Leftrightarrow {f}'\left( 1-\frac{x}{2} \right)>2\,\,\,\,\,\,\,\,\,\left( * \right).\)
Thử lần lượt từng đáp án.
Đáp án A: \(x\in \left( 2;4 \right)\Leftrightarrow 1-\frac{x}{2}\in \left( -1;0 \right)\Rightarrow f'\left( 1-\frac{x}{2} \right)>1\Rightarrow \) đáp án A sai.
Đáp án B: \(x\in \left( -4;-2 \right)\Leftrightarrow 1-\frac{x}{2}\in \left( 2;3 \right)\Rightarrow f'\left( 1-\frac{x}{2} \right)>2\Rightarrow B\) đúng.
Đáp án C: \(x\in \left( -2;0 \right)\Rightarrow 1-\frac{x}{2}\in \left( 1;2 \right)\Rightarrow -1<f'\left( 1-\frac{x}{2} \right)<2\Rightarrow C\) sai
Đáp án D: \(x\in \left( 0;2 \right)\Rightarrow 1-\frac{x}{2}\in \left( 0;1 \right)\Rightarrow -1<f'\left( 1-\frac{x}{2} \right)<1\Rightarrow D\) sai.
Chọn B.