Phương pháp giải:

+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \({{x}_{0}}:\,\,y=y'\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right)+{{y}_{0}}\).

+) Thay tọa độ điểm B vào phương trình tiếp tuyến, suy ra phương trình có dạng \(b=f\left( {{x}_{0}} \right)\), tìm điều kiện của b để phương trình đó có nghiệm duy nhất.

+) Phương trình \(b=f\left( {{x}_{0}} \right)\) có nghiệm duy nhất khi và chỉ khi đường thẳng \(y=b\) cắt đồ thị hàm số \(y=f\left( {{x}_{0}} \right)\) tại một điểm duy nhất. Lập BBT của đồ thị hàm số \(y=f\left( {{x}_{0}} \right)\) và kết luận.

Lời giải chi tiết:

Phương trình tiếp tuyến của \(\left( C \right)\) tại \(M\left( {{x}_{0}};x_{0}^{3}-3x_{0}^{2} \right)\)có dạng: \(y=\left( 3x_{0}^{2}-6{{x}_{0}} \right)\left( x-{{x}_{0}} \right)+x_{0}^{3}-3x_{0}^{2}\)

Do tiếp tuyến đi qua điểm \(\left( 0;b \right)\Rightarrow b=\left( 3x_{0}^{2}-6{{x}_{0}} \right)\left( -{{x}_{0}} \right)+x_{0}^{3}-3x_{0}^{2}=-2x_{0}^{3}+3x_{0}^{2}\)

Để có đúng một tiếp tuyến của \(\left( C \right)\) đi qua \(B\left( 0;b \right)\) thì phương trình \(b=-2x_{0}^{3}+3x_{0}^{2}\) có duy nhất một nghiệm. Xét hàm số \(y=-2{{x}^{3}}+3{{x}^{2}}\Rightarrow y'=-6{{x}^{2}}+6x=0\Leftrightarrow \left[ \begin{align}  & x=0\Rightarrow y=0 \\  & x=1\Rightarrow y=1 \\ \end{align} \right.\)

BBT:

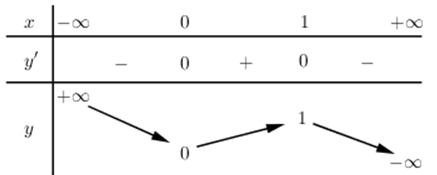
Dựa vào BBT của đồ thị hàm số suy ra PT có 1 nghiệm khi \(\left[ \begin{align}  & b>1 \\  & b<0 \\ \end{align} \right.\)

Với \(b\in \left( -10;10 \right)\Rightarrow b\in \left\{ -9;-8;-7;-6;-5;-4;-3;-2;-1;2;3;4;5;6;7;8;9 \right\}\Rightarrow \) có 17 giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.

Chọn A.