Câu hỏi
Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác vuông, \(AB=BC=a.\) Biết rằng góc giữa hai mặt phẳng \((AC{C}')\) và \((A{B}'{C}')\) bằng \({{60}^{0}}\) (tham khảo hình vẽ bên). Thể tích của khối chóp \({B}'.AC{C}'{A}'\) bằng
- A \(\frac{{{a}^{3}}}{3}.\)
- B \(\frac{{{a}^{3}}}{6}.\)
- C \(\frac{{{a}^{3}}}{2}.\)
- D \(\frac{\sqrt{3}{{a}^{3}}}{3}.\)
Phương pháp giải:
\({{V}_{B'.ACC'A'}}=V-{{V}_{B'.BAC}}=\frac{2}{3}V\), với V là thể tích khối lăng trụ.
Tính thể tích khối lăng trụ.
Lời giải chi tiết:
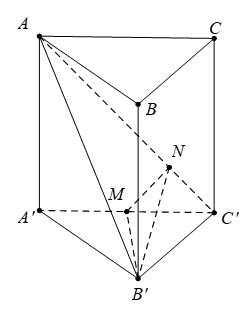
Dựng \(B'M\bot A'C'\Rightarrow B'M\bot \left( ACC'A' \right)\)
Dựng \(MN\bot AC'\Rightarrow AC'\bot \left( MNB' \right)\)
Khi đó \(\widehat{\left( \left( AB'C' \right);\left( AC'A' \right) \right)}=\widehat{MNB'}={{60}^{0}}\)
Ta có: \(B'M=\frac{a\sqrt{2}}{2}\Rightarrow MN=\frac{B'M}{\tan \widehat{MNB'}}=\frac{a\sqrt{6}}{6}\)
Mặt khác \(\tan \widehat{AC'A'}=\frac{MN}{C'N}=\frac{AA'}{A'C'}\)
Trong đó \(MN=\frac{a\sqrt{6}}{6};MC'=\frac{a\sqrt{2}}{2}\Rightarrow C'N=\sqrt{C'{{M}^{2}}-M{{N}^{2}}}=\frac{a\sqrt{3}}{3}\)
Suy ra \(AA'=a\)
Thể tích lăng trụ \(V=\frac{A{{B}^{2}}}{2}.AA'=\frac{{{a}^{3}}}{2}\)\(\Rightarrow {{V}_{B'.ACC'A'}}=V-{{V}_{B'.BAC}}=V-\frac{V}{3}=\frac{2}{3}V=\frac{{{a}^{3}}}{3}.\)
Chọn A.