Câu hỏi
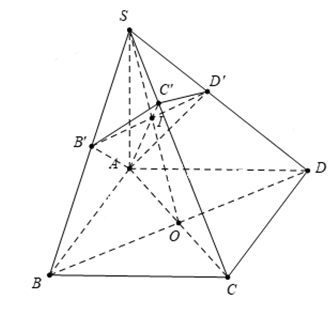
Cho hình chóp \(S.ABCD\)có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy
\(SA=a\sqrt{2}.\) Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp \(S.AB'C'D'\) là:
- A \(V=\frac{2{{a}^{3}}\sqrt{3}}{9}\)
- B \(V=\frac{2{{a}^{3}}\sqrt{2}}{3}\)
- C \(V=\frac{{{a}^{3}}\sqrt{2}}{9}\)
- D \(V=\frac{2{{a}^{3}}\sqrt{3}}{3}\)
Phương pháp giải:
+) Dựng thiết diện của hình chóp khi cắt bởi mặt phẳng (AB’D’), suy ra điểm C’.
+) Sử dụng tỉ số thể tích.
Lời giải chi tiết:
Gọi O là tâm hình vuông ABCD.
\(I=SO\cap B'D'\Rightarrow C'=AI'\cap SC.\)
Ta có: \(\left\{ \begin{align} & BC\bot AB \\ & BC\bot SA \\ \end{align} \right.\Rightarrow BC\bot AB'\)
Lại có \(AB'\bot SB\Rightarrow AB\bot 'SC\), tương tự \(AD'\bot SC\)
Do đó \(AC'\bot SC\)
Xét tam giác SAB có:
\(SB'.SB=S{{A}^{2}}\Rightarrow \frac{SB'}{SB}=\frac{S{{A}^{2}}}{S{{B}^{2}}}=\frac{S{{A}^{2}}}{S{{A}^{2}}+A{{B}^{2}}}=\frac{2}{3}\)
Tương tự \(\frac{SC'}{SC}=\frac{S{{A}^{2}}}{S{{C}^{2}}}=\frac{S{{A}^{2}}}{S{{A}^{2}}+A{{C}^{2}}}=\frac{2}{4}\)
Do đó \(\frac{{{V}_{S.AB'C'}}}{{{V}_{S.ABC}}}=\frac{2}{3}.\frac{2}{4}=\frac{1}{3},\) do tính chất đối xứng nên:\(\frac{{{V}_{S.AB'C'D'}}}{{{V}_{S.ABCD}}}=\frac{1}{3};{{V}_{S.ABCD}}=\frac{{{a}^{3}}\sqrt{2}}{3}\Rightarrow V=\frac{{{a}^{3}}\sqrt{2}}{9}.\)
Đáp án C