Câu hỏi
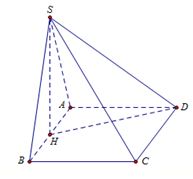
Cho hình chóp \(S.ABCD\)có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên \(SD=\frac{3a}{2}.\) Tính thể tích khối chóp \(S.ABCD\) theo a.
- A \(\frac{1}{3}{{a}^{3}}\)
- B \(\frac{\sqrt{3}}{3}{{a}^{3}}\)
- C \(\frac{\sqrt{5}}{3}{{a}^{3}}\)
- D \(\frac{\sqrt{2}}{3}{{a}^{3}}\)
Phương pháp giải:
Gọi H là trung điểm cạnh AB ta có \({{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}\)
Lời giải chi tiết:
Ta có \(HD=\sqrt{{{a}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{5}}{2}\)
\(SH=\sqrt{{{\left( \frac{3a}{2} \right)}^{2}}-{{\left( \frac{a\sqrt{5}}{2} \right)}^{2}}}=a\)
Thể tích khối chóp S.ABCD là: \(V=\frac{1}{3}{{S}_{ABCD}}.SH=\frac{1}{3}{{a}^{2}}.a=\frac{{{a}^{3}}}{3}.\)
Đáp án A.
Câu hỏi trước
