Môn Lý - Lớp 12
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 1)
Câu hỏi
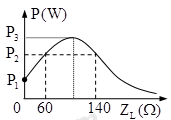
Đặt một điện áp xoay chiều \(u = U\sqrt 2 \cos (100\pi t)\) (U không đổi) vào hai đầu đoạn mạch nối tiếp gồm điện trở R, tụ điện có điện dung C và cuộn cảm có điện trở r = \(10\sqrt 2 \Omega \) , hệ số tự cảm L biến thiên. Đồ thị biểu diễn sự biến thiên của công suất tiêu thụ trên trên toàn mạch theo cảm kháng được cho như hình vẽ. Biết P3/P1 = 3, giá trị của điện trở R là:
- A \(40\sqrt 2 \Omega \)
- B \(50\sqrt 2 \Omega \)
- C 100Ω
- D \(100\sqrt 2 \Omega \)
Phương pháp giải:
Áp dụng định luật Ôm và điều kiện cộng hưởng
Lời giải chi tiết:
Từ đồ thị ta thấy có hai giá trị của ZL là 60Ω và 140Ω cùng cho 1 giá trị P.
Vị trí P3 đạt cực đại ứng với trường hợp cộng hưởng điện ZL = ZC
Và có mối quan hệ giữa ZL3 với ZL1 và ZL2 là: \({Z_{L3}} = {{{Z_{L1}} + {Z_{L2}}} \over 2} = {{60 + 140} \over 2} = 100\Omega \)
Khi ZL =0 thì mạch có công suất P1 thỏa mãn P3 /P1 = 3. Ta có:
\(\eqalign{
& {{{P_3}} \over {{P_1}}} = {{I_3^2.R} \over {{I^2}.R}} = 3 \Rightarrow {{{I_3}} \over I} = \sqrt 3 \Rightarrow {{{U \over {R + r}}} \over {{U \over {\sqrt {{{(R + r)}^2} + Z_C^2} }}}} = \sqrt 3 \Leftrightarrow {{\sqrt {{{(R + r)}^2} + Z_C^2} } \over {R + r}} = \sqrt 3 \Rightarrow {{{{(R + r)}^2} + Z_C^2} \over {{{(R + r)}^2}}} = 3 \cr
& \Rightarrow {Z_C} = \sqrt 2 .(R + r) = 100\Omega \Rightarrow R = {{100} \over {\sqrt 2 }} - 10\sqrt 2 = 50\sqrt 2 - 10\sqrt 2 = 40\sqrt 2 \Omega \cr} \)
Câu hỏi trước
