Câu hỏi
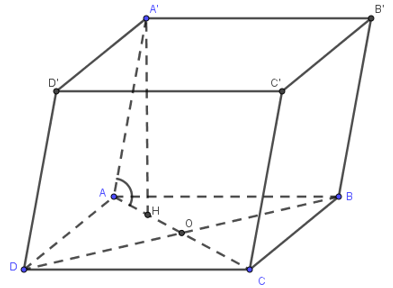
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi tâm O, cạnh bằng a, \(B'D'=a\sqrt{3}\). Góc giữa CC’ và mặt đáy là \({{60}^{0}}\), trung điểm H của AO là hình chiếu vuông góc của A’ lên mặt phẳng ABCD. Tính thể tích của hình hộp.
- A \(\frac{3}{4}{{a}^{3}}\).
- B \(\frac{{{a}^{3}}\sqrt{3}}{8}\).
- C \(\frac{{{a}^{3}}}{8}\).
- D \(\frac{3{{a}^{3}}}{8}\).
Phương pháp giải:
Thể tích hình hộp \(V=Bh\), trong đó:
\(B:\)diện tích đáy,
\(h:\) chiều cao.
Lời giải chi tiết:
Do AA’ // CC’ nên \(\left( \widehat{A\,A'},(ABCD) \right)=\left( \widehat{CC'},(ABCD) \right)={{60}^{0}}\).\(A'H\bot (ABCD),\,\,H\in (ABCD)\Rightarrow \left( \widehat{AA',(ABCD)} \right)=\widehat{A'AH}={{60}^{0}}\)
Hình thoi ABCD có AB = BC = CD = DA = a, \(BD=B'D'=a\sqrt{3}\)
Tam giác OAB vuông tại O:
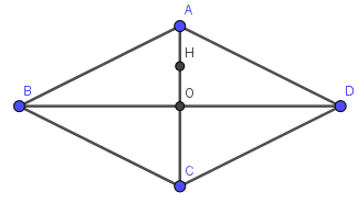
Diện tích hình thoi ABCD: \({{S}_{ABCD}}=\frac{1}{2}AC.BD=\frac{1}{2}.a.a\sqrt{3}=\frac{{{a}^{2}}\sqrt{3}}{2}\)
Tam giác A’AH vuông tại H: \(\tan \widehat{A'AH}=\frac{A'H}{AH}\Leftrightarrow \tan {{60}^{0}}=\frac{A'H}{\frac{a}{4}}\Leftrightarrow A'H=\frac{a\sqrt{3}}{4}\)
Thể tích hình hộp ABCD.A’B’C’D’: \(V = {S_{ABCD}}.A'H = \frac{{{a^2}\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{4} = \frac{{3{a^3}}}{8}\).
Chọn: D