Câu hỏi
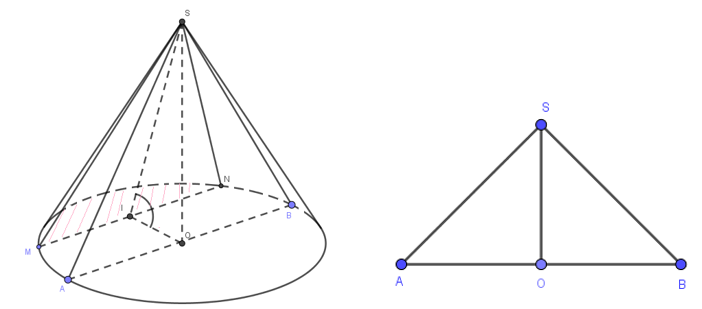
Một khối nón có thiết diện qua trục là một tam giác vuông cân và đường sinh có độ dài bằng \(3\sqrt{2}\)cm. Một mặt phẳng đi qua đỉnh và tạo với đáy một góc \({{60}^{0}}\) chia khối nón thành hai phần. Tính thể tích phần nhỏ hơn (Tính gần đúng đến hàng phần trăm).
- A \(4,36\,c{{m}^{3}}\).
- B \(5,37\,c{{m}^{3}}\).
- C \(5,61\,c{{m}^{3}}\).
- D \(4,53\,c{{m}^{3}}\).
Phương pháp giải:
- Xác định góc giữa mặt phẳng và mặt phẳng.
- Lập tỉ lệ thể tích thông qua tỉ lệ diện tích đáy và tỉ lệ chiều cao.
Lời giải chi tiết:
Xét hình nón (H) thỏa mãn yêu cầu đề bài, có một thiết diện qua trục là tam giác SAB.
Ta có: SAB cân tại S và là tam giác vuông cân \(\Rightarrow \Delta SAB\) vuông cân tại đỉnh S.
Gọi O là trung điểm của AB \(\Rightarrow SO=OA=OB=\frac{SA}{\sqrt{2}}=\frac{3\sqrt{2}}{\sqrt{2}}=3\,\,(cm)\)
Thể tích hình nón (H): \(V=\frac{1}{3}SO.\pi .O{{A}^{2}}=\frac{1}{3}.3.\pi {{.3}^{2}}=9\pi \)
Gọi (P) là một mặt phẳng đi qua đỉnh và tạo với đáy một góc \({{60}^{0}}\), thiết diện của (P) với mặt đáy là tam giác cân SMN.
Gọi I là trung điểm của MN (hiển nhiên I không trùng O), suy ra \(IO\bot MN\)
Mà \(SO\bot MN\), (vì \(SO\bot \) đáy).
\(\Rightarrow MN\bot (SIO)\) \(\Rightarrow \left( \widehat{(P),(ABI)} \right)=\widehat{OIS}={{60}^{0}}\) .
Tam giác SIO vuông tại O \(\Rightarrow IO=\frac{SO}{\tan \widehat{SIO}}=\frac{SO}{\tan {{60}^{0}}}=\frac{3}{\sqrt{3}}=\sqrt{3}\,\,(cm)\)
Gọi \({{V}_{0}}\) là thể tích của phần nhỏ hơn. Ta có: \(\frac{{{V}_{0}}}{V}=\frac{\frac{1}{3}{{S}_{0}}.h}{\frac{1}{3}S.h}=\frac{{{S}_{0}}}{S}\Rightarrow {{V}_{0}}=V.\frac{{{S}_{0}}}{S}\)
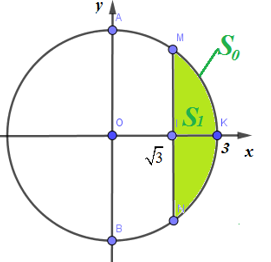
*) Tính diện tích đáy của phần có thể tích nhỏ hơn:
Diện tích hình tròn \(S=\pi O{{A}^{2}}=\pi {{.3}^{2}}=9\pi \)
\({{S}_{0}}=2{{S}_{1}}=2\int\limits_{\sqrt{3}}^{3}{\sqrt{9-{{x}^{2}}}dx}\)
Đặt \(x=3\sin t\Rightarrow dx=3\cos tdt\)
Đổi cận:
\(\begin{align} & x=\sqrt{3}\to t=arc\,\sin \frac{1}{\sqrt{3}} \\ & x=3\,\,\,\,\,\,\to t=\frac{\pi }{2} \\\end{align}\)
\(\begin{align} & \Rightarrow {{S}_{0}}=2\int\limits_{\sqrt{3}}^{3}{\sqrt{9-{{x}^{2}}}dx}=2\int\limits_{a\,rc\sin \frac{1}{\sqrt{3}}}^{\frac{\pi }{2}}{\sqrt{9-9{{\sin }^{2}}t}.3\cos t.dt}=18\int\limits_{a\,rc\sin \frac{1}{\sqrt{3}}}^{\frac{\pi }{2}}{{{\cos }^{2}}t.dt}=18\int\limits_{a\,rc\sin \frac{1}{\sqrt{3}}}^{\frac{\pi }{2}}{\frac{1+\cos 2t}{2}.dt}=\left. \left( 9t+\frac{9}{2}\sin 2t \right) \right|_{a\,rc\sin \frac{1}{\sqrt{3}}}^{\frac{\pi }{2}} \\ & =\frac{9\pi }{2}-9a\,rc\sin \frac{1}{\sqrt{3}}-\frac{9}{2}\sin (2a\,rc\sin \frac{1}{\sqrt{3}}) \\\end{align}\)\(\begin{align} & \Rightarrow \frac{{{S}_{0}}}{S}=\frac{\frac{9\pi }{2}-9a\,rc\sin \frac{1}{\sqrt{3}}-\frac{9}{2}\sin (2a\,rc\sin \frac{1}{\sqrt{3}})}{9\pi } \\ & \Rightarrow {{V}_{0}}=V.\frac{{{S}_{0}}}{S}=9\pi .\frac{\frac{9\pi }{2}-9a\,rc\sin \frac{1}{\sqrt{3}}-\frac{9}{2}\sin (2a\,rc\sin \frac{1}{\sqrt{3}})}{9\pi }\approx 4,36\,(c{{m}^{3}}) \\\end{align}\)
Chọn: A