Câu hỏi
Cho khối chóp \(S.ABC\) có \(\widehat{BAC}={{90}^{0}},BC=2\sqrt{2},\widehat{ACB}={{30}^{0}},\) hình chiếu của \(S\) trên mặt phẳng đáy là trung điểm \(H\) của \(BC\). Giả sử có mặt cầu tâm \(O\), bán kính bằng 1 tiếp xúc với \(SA,SB,SC\) lần lượt tại các điểm \({{A}_{1}},{{B}_{1}},{{C}_{1}}\), trong đó \({{A}_{1}},{{B}_{1}}\) thuộc các cạnh tương ứng \(SA,SB\), còn \({{C}_{1}}\) thuộc tia đối của tia \(SC\); đồng thời mặt cầu tâm \(O\) đó tiếp xúc với mặt phẳng \(\left( ABC \right)\). Thể tích của hình chóp \(S.ABC\) là
- A \(\frac{2\sqrt{2}}{3}.\)
- B \(\frac{\sqrt{3}}{3}.\)
- C \(\frac{2\sqrt{3}}{3}.\)
- D \(\frac{3\sqrt{2}}{2}.\)
Phương pháp giải:
Dựng hình, xác định bán kính mặt cầu để suy ra chiều cao của khối chóp
Lời giải chi tiết:
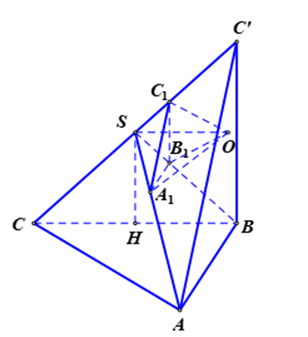
Do mặt cầu tâm \(O\) tiếp xúc với \(SA,\ SB,\ SC\) lần lượt tại các điểm \({{A}_{1}},\ {{B}_{1}},\ {{C}_{1}}\Rightarrow S{{A}_{1}}=S{{B}_{1}}=S{{C}_{1}}\) \(\left( 1 \right)\).
Mặt khác ta có \(O{{A}_{1}}=O{{B}_{1}}=O{{C}_{1}}\) \(\left( 2 \right)\).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(SO\bot \left( {{A}_{1}}{{B}_{1}}{{C}_{1}} \right)\).
Gọi \({C}'\) là điểm đối xứng của \(C\) qua \(S\).
Ta có các tam giác \(SAB,\ SA{C}',\ SB{C}'\) cân tại \(S\).
Suy ra \({{A}_{1}}{{B}_{1}}\text{//}AB,\,\,{{A}_{1}}{{C}_{1}}\text{//}A{C}',\,\,{{B}_{1}}{{C}_{1}}\text{//}B{C}'\)\(\Rightarrow \left( {{A}_{1}}{{B}_{1}}{{C}_{1}} \right)\text{//}\left( AB{C}' \right)\)
\(SH\text{//}B{C}'\Rightarrow SH\text{//}\left( AB{C}' \right)\). Vậy \(SO\bot SH.\)
\(\Rightarrow SH=d\left( O,\left( ABC \right) \right)=R=1\). Vậy \(V=\frac{\sqrt{3}}{3}.\)
Chọn B