Câu hỏi
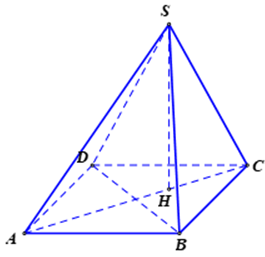
Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(a\),\(\widehat{BAD}={{60}^{0}}\), các mặt bên \(\left( SAB \right)\), \(\left( SAD \right)\) và \(\left( SBD \right)\) tạo với đáy một góc bằng \({{45}^{0}}\). Thể tích của khối chóp có giá trị lớn nhất là
- A \(\frac{{{a}^{3}}}{4}.\)
- B \(\frac{{{a}^{3}}}{3}.\)
- C \(\frac{{{a}^{3}}}{6}.\)
- D \(\frac{{{a}^{3}}}{2}.\)
Phương pháp giải:
Xác định thể tích khối chóp bằng cách xác định chiều cao, với hình chiếu của đỉnh là tâm đường tròn nội tiếp hoặc ngoại tiếp tam giác đáy
Lời giải chi tiết:
Ba mặt bên \(\left( SAB \right),\left( SAD \right),\left( SBD \right)\) tạo với đáy các góc bằng nhau và bằng \({{45}^{0}}.\)
\(\Rightarrow \) Chân đường cao trùng tâm đường tròn nội tiếp \(\Delta \,ABD\) hoặc chân đường cao trùng với đường tròn tâm bàng tiếp của \(\Delta \,ABD\).
Xét 2 trường hợp ta nhận thấy thể tích khối chóp lớn nhất \(\Rightarrow \) \({{V}_{max}}\) khi chân đường cao trùng tâm bàng tiếp \(\Delta ABD \Rightarrow H \equiv C.\)
Ta có \(\widehat {DAB} = {60^0} \Rightarrow \Delta ABD\) là tam giác đều cạnh \(a.\)
\( \Rightarrow {S_{ABCD}} = 2{S_{ABD}} = 2.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{2}.\)
Ta có: \(\widehat {\left( {\left( {SBD} \right),\;\left( {ABCD} \right)} \right)} = \widehat {\left( {SO,\;OC} \right)} = \widehat {SOC} = {45^0}.\)
\( \Rightarrow \Delta SOC\) vuông cân tại \(C \Rightarrow SC = OC = \frac{{a\sqrt 3 }}{2}.\)
\( \Rightarrow {V_{max}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}}}{4}.\)
Chọn C