Câu hỏi
Cho hai số phức \(z=2+3i,z'=3-2i\). Tìm môđun của số phức \(w=z.z'\).
- A \(\left| w \right|=\sqrt{13}\)
- B \(\left| w \right|=13\)
- C \(\left| w \right|=12\)
- D \(\left| w \right|=14\)
Phương pháp giải:
Tính \(z.z'\Rightarrow w\)
Tính môđun của số phức \(w=a+bi\): \(\left| w \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\)
Lời giải chi tiết:
Sử dụng MTCT ta tính được:
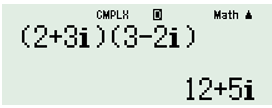
\(\Rightarrow w=z.z'=12+5i.\)
\(\Rightarrow \left| w \right|=\sqrt{{{12}^{2}}+{{5}^{2}}}=13\).
Chọn B.
Câu hỏi trước
