Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên. Phát biểu nào dưới đây là SAI ?
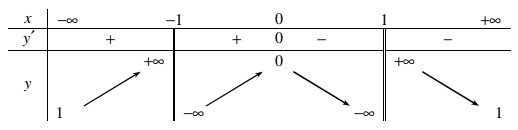
- A Đồ thị hàm số nhận gốc tọa độ O làm điểm cực đại.
- B Đồ thị hàm số có ba đường tiệm cận.
- C Đồ thị hàm số cắt đường thẳng \(y = 2018\) tại hai điểm phân biệt.
- D Hàm số đồng biến trên \(\left( { - \infty ;0} \right)\) và nghịch biến trên \(\left( {0; + \infty } \right)\)
Phương pháp giải:
Dựa vào các khái niệm cực trị, đường tiệm cận, khoảng đơn điệu của đồ thị hàm số.
Lời giải chi tiết:
A đúng vì \(y'\left( 0 \right) = 0\) và qua điểm \(x = 0\) thì y’ đổi dấu từ dương sang âm.
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = - \infty ,\,\,\mathop {\lim }\limits_{x \to - {1^ - }} y = + \infty \Rightarrow x = 1\) là TCĐ của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty ,\,\,\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty \Rightarrow x = - 1\) là TCĐ của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to \infty } y = 1 \Rightarrow y = 1\) là TCN của đồ thị hàm số.
Hàm số có 3 đường tiệm cận \( \Rightarrow B\) đúng.
C hiển nhiên đúng.
Chọn D.







