Câu hỏi
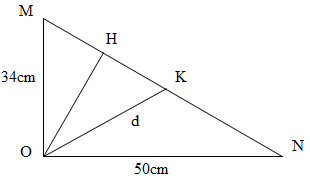
Một nguồn sóng đặt tại điểm O trên mặt nước, dao động theo phương vuông góc với mặt nước với phương trình u = acos40πt (cm), trong đó t tính theo giây. Gọi M và N là hai điểm nằm trên mặt nước sao cho OM vuông góc với ON. Biết tốc độ truyền sóng trên mặt nước bằng 80cm/s. Khoảng cách từ O đến M và N lần lượt là 34cm và 50cm. Số phần tử trên đoạn MN dao động cùng pha với nguồn là
- A 5
- B 7
- C 6
- D 4
Phương pháp giải:
Độ lệch pha: \(\Delta \varphi = {{2\pi d} \over \lambda }\)
Lời giải chi tiết:
+ Áp dụng hệ thức lượng trong tam giác vuông OMN có đường cao OH:
\({1 \over {O{H^2}}} = {1 \over {O{M^2}}} + {1 \over {O{N^2}}} \Leftrightarrow {1 \over {O{H^2}}} = {1 \over {{{34}^2}}} + {1 \over {{{50}^2}}} \Rightarrow OH = 28,1cm\)
+ Gọi d là khoảng cách từ O đến K (K là 1 điểm bất kì trên MN)
+ Độ lệch pha giữa K và O là : \(\Delta \varphi = {{2\pi d} \over \lambda }\)
+ Để K dao động cùng pha với O thì : \(\Delta \varphi = {{2\pi d} \over \lambda } = 2k\pi \Rightarrow d = k\lambda \)
+ Số điểm dao động cùng pha với o trên đoạn MN bằng số giá trị k nguyên thoả mãn :
\(\left\{ \matrix{
28,1 \le k\lambda \le 34 \Rightarrow 7,025 \le k \le 8,5 \Rightarrow k = 8 \hfill \cr
28,1 < k\lambda \le 50 \Rightarrow 7,025 < k \le 12,5 \Rightarrow k = 8;9;10;11;12 \hfill \cr} \right.\)
Có 6 giá trị của k thoả mãn => trên đoạn MN có 6 điểm dao động cùng pha với nguồn