Câu hỏi
Cho ba tập hợp:
\(A = \left\{ {x \in \mathbb{R}| - 3 < x < 1} \right\};\,\,\,\,B = \left\{ {x \in \mathbb{R}| - 1 \le x \le 5} \right\};\,\,C = \left\{ {x \in \mathbb{R}|\left| x \right| \ge 2} \right\}.\)
Xác định các tập hợp sau: \(\left( {A \cup B} \right) \cup C;\,\,\,\,\left( {A \cap B} \right) \cap C;\,\,\left( {A \cap C} \right) \cup B.\)
- A Các tập hợp lần lượt là: R; (-3;-2]; (-3;-2]
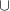[2;5]; (-3;-2]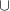[-1;5] - B Các tập hợp lần lượt là: R; rỗng; (-3;-2]
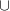[1;5]; (-3;-2]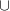[-1;5] - C Các tập hợp lần lượt là: R; rỗng; (-3;-2]
(2;5); (-3;-2][-1;5] - D Các tập hợp lần lượt là: R; rỗng; (-3;-2]
[2;5]; (-3;-2][-1;5]
Lời giải chi tiết:
Ta có : \(A = \left( { - 3;\,\,1} \right);\,\,\,B = \left[ { - 1;\,\,5} \right];\,\,\,C = \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right).\) Do đó :
\(\begin{array}{l} + )\,\,\,A \cup B = \left( { - 3;\,\,5} \right] \Rightarrow A \cup B \cup C = \mathbb{R}.\\ + )\,\,A \cap B = \left[ { - 1;\,\,1} \right) \Rightarrow A \cap B \cap C = \emptyset \\ + )\,\,\left( {A \cup B} \right) \cap C = \left( { - 3; - 2} \right] \cup \left[ {2;\,\,5} \right]\\ + )\,\,A \cap C = \left( { - 3;\, - 2} \right] \Rightarrow \left( {A \cap C} \right) \cup B = \left( { - 3; - 2} \right] \cup \left[ { - 1;\,\,5} \right].\end{array}\)
Câu hỏi trước
